【目次】

ラビット・チャレンジの受講レポート。

プロローグ

識別と生成

  識別モデル
(discriminative, backward)		 生成モデル
(generative, forward)
目的 データを目的のクラスに分類する 特定のクラスのデータを生成する
計算結果 $p(C_k | x)$ $p(x | C_k)$
具体的なモデル 決定木
ロジスティック回帰
SVM
NN		 HMM
ベイジアンネットワーク
VAE
GAN
特徴 高次元→低次元
必要な学習データ：少		 低次元→高次元
必要な学習データ：多

識別機(Clasifier)の開発アプローチ

  生成モデル 識別モデル 識別関数
識別の計算 $p(x | C_k) \cdot p(c_k)$を推定
ベイズの定理より
$p(C_k | x) = \frac{p(x | C_k) \cdot p(C_k)}{p(x)}$
ただし$p(x) = \sum_{k}p(x | C_k) p(C_k)$		 $p(C_k | x)$を推定
決定理論に基づき識別結果を得る
(閾値に基づく決定など)		 入力値$x$を直接クラスに写像(変換)する関数$f(x)$を推定
モデル化の対象 各クラスの生起確率
データのクラス条件付き密度		 データがクラスに属する確率 データの属するクラスの情報のみ
確率は計算されない
特徴 データを人工的に生成できる
確率的な識別		 確率的な識別 学習量が少ない
決定的な識別

参考：「パターン認識と機械学習」(2007年)
→生成モデルの研究が発達する前の分類方法

識別器における生成モデルと識別モデル

  • 生成モデル
    • データのクラス条件付き密度の分布を推定
      • 分類結果より複雑、計算量が多い
  • 識別モデル
    • 直接データがクラスに属する確率を求める

識別器における識別モデルと識別関数

  • 識別モデル
    • 入力データから事後確率を推論して識別結果を決定
    • 識別結果の確率が得られる
  • 識別関数
    • 識別結果のみ得られる

万能近似定理と深さ

活性化関数をもつネットワークを使うことで、どんな関数でも近似できるのでは？という定理


Day1: NN

ニューラルネットワークの全体像

入力層→中間層→出力層

確認テスト1

  • ディープラーニングは何をしようとしているか？
    • 自分の解答
      • 人間が具体的な数学モデルを直接構築するのではなく、ニューラルネットワークが入力データから特徴量を抽出することで、数学モデルを構築する
    • 模範解答
      • 明示的なプログラムの代わりに多数の中間層を持つニューラルネットワークを用いて、入力値から目的とする出力値に変換するを数学モデルを構築すること。
  • どの値の最適化が最終目標か？
    • 重み(W), バイアス(b)

確認テスト2

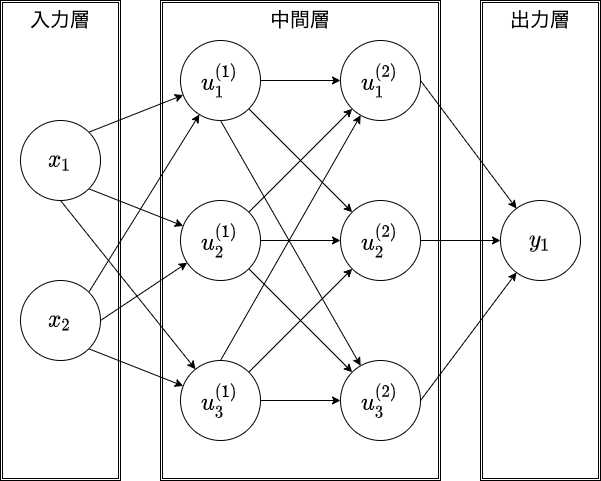
次のネットワークを描く

  • 入力層：2ノード1層
  • 中間層：3ノード2層
  • 出力層：1ノード1層

test_2

  • NNの対象とする問題の種類
    • 回帰
    • 分類

入力層〜中間層

$u = Wx + b$

1次関数において、

  • $W$: 傾き
  • $b$: 切片 bias

$W, b$を学習する

確認テスト3

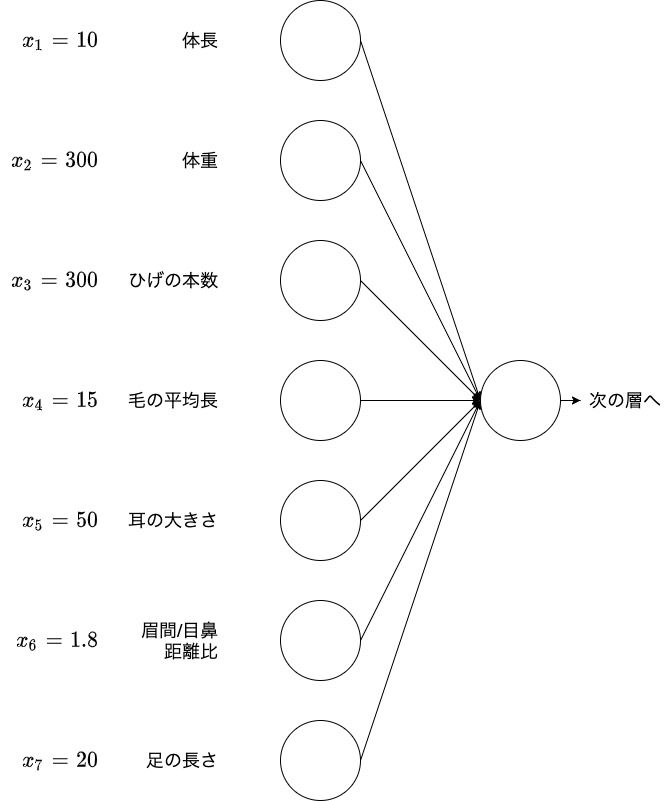
test_3

確認テスト

  • 以下の数式をPythonで書く
    $u = Wx + b$
u = np.dot(x, W) + b
  • 中間層の出力を定義しているソース
# 2層の総入力
u2 = np.dot(z1, W2) + b2

# 2層の総出力
z2 = functions.relu(u2)

活性化関数

次の層への出力の大きさを決める非線形の関数
次の層への信号のON/OFFや強弱を定める

確認テスト

線形と非線形の違い

  • 線形：直線
    • 加法性と斉次性を満たす
  • 非線形：非直線
    • 加法性と斉次性を満たさない

中間層用の活性化関数

  • ReLU関数
    • 勾配消失問題の回避とスパース化
      • スパース化するとモデルの中身がシンプルになる
    \[f(x) = \left\{ \begin{array}{ll} x & (x > 0) \\ 0 & (x \leqq 0) \\ \end{array} \right.\] 
      # プログラム例
  def relu(x):
      return np.maximum(0, x)
  • シグモイド(ロジスティック)関数
    • 勾配消失問題
    \[f(u) = \frac{1}{1 + e^{-u}}\] 
      # プログラム例
  def sigmoid(x):
      return 1 / (1 + np.exp(-x))
  • ステップ関数
    • 線形分離可能なものしか学習できない
    \[f(x) = \left\{ \begin{array}{ll} 1 & (x \geqq 0) \\ 0 & (x < 0) \\ \end{array} \right.\] 
      # プログラム例
  def step_function(x):
      if x > 0:
          return 1
      else:
          return 0

確認テスト

ソースコードのうち、以下に該当する箇所を抜き出す

\[z = f(u)\] 
# 1層の総出力
z1 = functions.relu(u1)

# 2層の総出力
z2 = functions.relu(u2)

出力層

  • 役割
    • 問題に対する判定結果を出力する
  • 誤差関数
    • 訓練データを入力し、NNの出力した判定結果と期待した判定結果の誤差を求める

    • 例：二乗誤差

      \[E_n(w) = \frac{1}{2} \sum_{j=1}^{J} (y_j - d_j)^2 = \frac{1}{2} ||(y - d)||^2\] 
        # 平均二乗誤差のコード例
  def mean_squared_error(d, y):
      return np.mean(np.square(d - y)) / 2

確認テスト

  • なぜ引き算ではなく二乗するか？
    • 引き算の場合正負の符号の差が出てしまい、全体の誤差を正しく表すのに都合が悪いため
    • 二乗してそれぞれのラベルでの誤差を正の値にする
  • 上記二乗誤差の式の$\frac{1}{2}$はどういう意味をもつか？
    • 誤差逆伝搬の計算において、誤差関数の微分を用いる際の計算を簡単にするため(本質的な意味はない)

出力層の活性化関数

  • ソフトマックス関数
  • 恒等写像
  • シグモイド関数

中間層との違い

  • 値の強弱
    • 中間層：しきい値の前後で信号の強弱を調整
    • 出力層：信号の大きさ(比率)はそのままに変換
  • 確率出力
    • 分類問題の場合、以下が必要
      • 出力層の出力は0~1の範囲に限定
      • 総和を1とする

出力層の種類 - 全結合NN

  回帰 二値分類 多クラス分類
活性化関数 恒等写像 シグモイド関数 ソフトマックス関数
誤差関数 二乗誤差 交差エントロピー 交差エントロピー

  • 恒等写像

    \[f(u) = u\]

  • シグモイド関数

    \[f(u) = \frac{1}{1 + e^{-u}}\] 
      # シグモイド関数
  def sigmoid(x):
      return 1 / (1 + np.exp(-x))

  • ソフトマックス関数

    \[f(i, u) = \frac{e^{u_i}}{\sum_{k=1}^{K} e^{u_k}}\] 
      # ソフトマックス関数
  def softmax(x): 
      if x.ndim == 2:
          # ミニバッチのときの処理
          x = x.T
          x = x - np.max(x, axis=0)
          y = np.exp(x) / np.sum(np.exp(x), axis=0)
          rerurn y.T
        
      x = x - np.max(x)   # オーバーフロー対策
      return np.exp(x) / np.sum(np.exp(x))

【訓練データサンプルあたりの誤差】

  • 二乗誤差 (実際には平均二乗誤差が用いられることが多い)

    \[E_n(W) = \frac{1}{2} \sum_{i=1}^{I} (y_n - d_n)^2\]

  • 交差エントロピー

    \[E_n(W) = - \sum_{i=1}^{I} d_i \log y_i\]

【学習サイクルあたりの誤差】

\[E(W) = \sum_{n=1}^{N} E_n\]

確認テスト

(1) ~ (3)の数式に該当するソースコードを示し、一行ずつ処理の説明をせよ

\[\overbrace{f(i, u)}^{(1)} = \frac{\overbrace{e^{u_i}}^{(2)} }{ \underbrace{\sum_{k=1}^{K} e^{u_k}}_{(3)} }\]
  • (1): def softmax(x):
  • (2): np.exp(x)
    • 1クラス分の確率
  • (3): np.sum(np.exp(x))
    • 全クラス分の確率の和
      $\space$

  • 各行の説明

      def softmax(x): 
      if x.ndim == 2:
          # ミニバッチのときの処理
          x = x.T                                     # 転置
          x = x - np.max(x, axis=0)                   # オーバーフロー対策
          y = np.exp(x) / np.sum(np.exp(x), axis=0)   # softmaxの値を計算する
          return y.T                                  # 転置して返す
        
      x = x - np.max(x)                               # オーバーフロー対策
      return np.exp(x) / np.sum(np.exp(x))            # softmaxの値を計算して返す

確認テスト

【交差エントロピー】

(1), (2)の数式に該当するソースコードを示し、1行ずつ処理の説明をせよ

\[\overbrace{E_n(w)}^{(1)} = \overbrace{- \sum_{i=1}^{I} d_i \log y_i}^{(2)}\]
  • (1): def cross_entropy_error(d, y):
  • (2): -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7))
    $\space$
  • 各行の説明 
      def cross_entropy_error(d, y):
      if y.ndim == 1:                 # 1次元行列の場合
          d = d.reshape(1, d.size)    # 2次元行列に変形
          y = y.reshape(1, y.size)    # 2次元行列に変形
        
      if d.size == y.size:
          # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
          d = d.argmax(axis=1)        # 配列内の最大要素のインデックスを取得
        
      batch_size = y.shape[0]         # バッチサイズを取得
      return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size # 交差エントロピーを計算して返す
    • y: 0か1の配列
    • batch_size: ミニバッチの何番目？
    • d: d番目は0 or 1?
    • 1e-7: 対数関数では0のとき$- \infty$に飛ぶ。これを防ぐための処理

勾配降下法

  • 勾配降下法
  • 確率的勾配降下法
  • ミニバッチ勾配降下法

パラメータ$w$を最適化
誤差を最小にする$w$を見つける

勾配降下法

全サンプルの平均誤差

\[w^{(t + 1)} = w^{(t)} - \epsilon \nabla E\\ \space \\ \nabla E = \frac{\partial E}{\partial w} = \biggl[ \frac{\partial E}{\partial w_1} \cdots \frac{\partial E}{\partial w_M} \biggr]\]

→前回の値$w^{(t)}$から誤差$\epsilon \nabla E$を引いた値が今回の値$w^{(t + 1)}$

【$\epsilon$：学習率】

  • 大きすぎる場合：
    • 最小値にたどり着かず、発散する
  • 小さすぎる場合：
    • 収束するまでに時間がかかる
    • 局所解に陥る場合あり

【認識に必要なデータ数】
画像分類：1クラスあたり1000~5000枚あると精度が出る
自然言語モデル：Wikipediaの全てのデータを100~200エポック学習すると、ある程度結果が出る

確率的勾配降下法 (SGD)

ランダムに抽出したサンプルの誤差

\[w^{(t + 1)} = w^{(t)} - \epsilon \nabla E_n\\\]

メリット：

  • データが冗長な場合の計算コスト軽減
  • 望まない局所極小解に収束するリスクを軽減
  • オンライン学習ができる

確認テスト

  • オンライン学習とは？
    • 学習データを入力すると、その都度パラメータを更新する
  • バッチ学習とは？
    • 予め全データを準備しておき、一気に全ての学習データを更新する

メモリの容量には限りがあるので、オンライン学習を使うことが多い

ミニバッチ勾配降下法

ミニバッチ$D_t$に属するサンプルの平均誤差
(ミニバッチ：ランダムに分割したデータの集合)

\[\begin{split} &w^{(t + 1)} = w^{(t)} - \epsilon \nabla E_t \\ &E_t = \frac{1}{N_t} \sum_{n \in D_t} E_n \\ &N_t = | D_t | \\ & (N_t: バッチ数) \end{split}\]

メリット：

  • 計算機の計算資源を有効利用
    • スレッド並列化(CPU)やSIMD並列化(GPU)
      • SIMD: Single Instruction Multi Data
        • 一つの命令を同時に並列実行
    • 各バッチに対する処理を並列にできる

確認テスト

以下の数式の意味を図に描いて説明せよ

\[w^{(t + 1)} = w^{(t)} - \epsilon \nabla E_t\]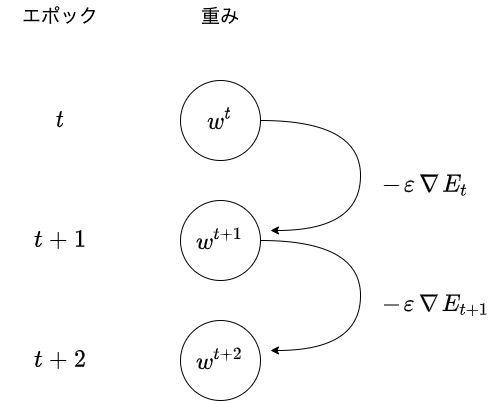

test_mini_batch

  1. 1エポック目を学習する
  2. 2エポック目は、1エポック目での間違いに学習率をかけた分を修正して学習する
  3. 3エポック目以降も、同様に学習していく

誤差勾配の計算

どう計算する？

\[\nabla E = \frac{\partial E}{\partial w} = \biggl[ \frac{\partial E}{\partial w_1} \cdots \frac{\partial E}{\partial w_M} \biggr]\]

【数値微分】
プログラムで微小な数値を生成し、擬似的に微分を計算する

\[\frac{\partial E}{\partial w_m} \approx \frac{E(w_m + h) - E(w_m - h)}{2h}\]

$h$: 微小な値
$m$番目の$w$を微小変化させた状態で、
全ての$w$について誤差$E$を計算

デメリット：計算量が多く、負荷が大きい

→代わりに誤差逆伝播法を利用する

誤差逆伝播法

算出された誤差を、出力層から順に微分し、前の層へ順に伝播
最小限の計算で各パラメータでの微分値を解析的に計算する方法

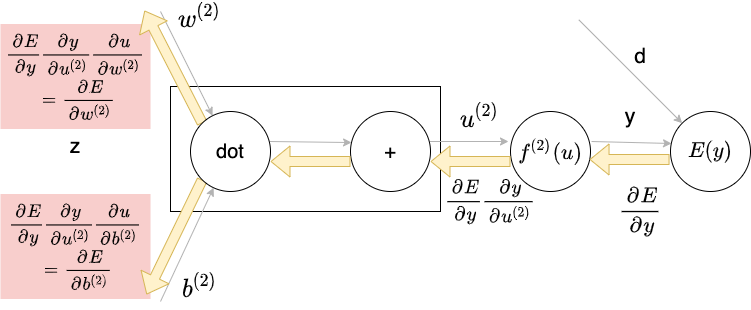
back_propagation

dとy(正解と予測結果)から誤差$E(y)$を計算する
誤差から微分を逆算する
→不要な再帰的計算を避けて微分を算出できる

確認テスト

すでに行った計算結果を保持するソースコードを抽出せよ

# 出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y)

【誤差勾配の計算】

\[\begin{array}{ll} E(y) = \frac{1}{2} \sum_{j=1}^{J} (y_j - d_j)^2 = \frac{1}{2} || y - d ||^2 & : 誤差関数 = 二乗誤差関数 \\ y = u^{(u)} & : 出力層の活性化関数 = 恒等写像 \\ u^{(l)} = w^{(l)} z{(l-1)} + b^{(l)} & : 総入力の計算 \end{array}\] \[\begin{split} &\frac{\partial E}{\partial w_{ji}^{(2)}} = \overbrace{ \frac{\partial E}{\partial y} }^{【1】} \overbrace{ \frac{\partial y}{\partial u} }^{【2】} \overbrace{ \frac{\partial u}{\partial w_{ji}^{(2)}} }^{【3】} \\ \space \\ &【1】\frac{\partial E(y)}{\partial y} = \frac{\partial}{\partial y} \frac{1}{2} || y - d ||^2 = y - d \\ &【2】\frac{\partial y(u)}{\partial u} = \frac{\partial u}{\partial u} = 1 \\ &【3】\frac{\partial u(w)}{\partial w_{ji}} = \frac{\partial}{\partial w_{ji}}(w^{(l)} z^{(l-1)} + b^{(l)}) = \frac{\partial}{\partial w_{ji}} \left( \left[ \begin{array}{c} w_{11} z_1 + \cdots + w_{1i z_i} + \cdots + w_{1I} z_I \\ \vdots \\ w_{j1} z_1 + \cdots + w_{ji z_i} + \cdots + w_{jI} z_I \\ \vdots \\ w_{J1} z_1 + \cdots + w_{Ji z_i} + \cdots + w_{JI} z_I \\ \end{array} \right] + \left[ \begin{array}{c} b_1 \\ \vdots \\ b_j \\ \vdots \\ b_J \\ \end{array} \right] \right) = \left[ \begin{array}{c} 0 \\ \vdots \\ z_i \\ \vdots \\ 0 \\ \end{array} \right] \end{split}\]

【3】：$w_{ji}$という一つの項目について微分している。そのため、その他の行は全て0になってしまう

\[\Rightarrow \frac{\partial E}{\partial w_{ji}^{(2)}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w_{ji}^{(2)}} = (y - d) \cdot 1 \cdot \left[ \begin{array}{c} 0 \\ \vdots \\ z_i \\ \vdots \\ 0 \end{array} \right] = (y_j - d_j) z_i\]

確認テスト

以下の数式に該当するソースコードを探せ

  • $\frac{\partial E}{\partial y}$
    • delta2 = functions.d_mean_squared_error(d, y)
  • $\frac{\partial E}{\partial y} \frac{\partial y}{\partial u}$
    • delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
  • $\frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w_{ji}^{(2)}}$
    • grad['W1'] = np.dot(x.T, delta1)

ディープラーニングの開発環境

  • ローカル (下にいくほど速い)
    • CPU ¥8,000程度
    • GPU ¥20,000程度
    • (FPGA) ¥100,000程度
      • 自分でプログラムできる計算機
      • あるプログラムだけ高速処理できる。他は遅い
    • ASIC(TPU) ¥数億
      • プログラム不可の計算機
      • あるプログラムを高速実行できるように工場で生産する
      • TPU(by Google)は機械学習用
  • クラウド
    • AWS
    • GCP
      • TPUを提供

その他のトピック

入力層の設計

  • 入力としてとり得るデータ (数値の集まり)
    • 連続する実数
    • 確率
    • フラグ値
  • 入力として取るべきでないデータ
    • 欠損値が多いデータ
    • 誤差が多いデータ
    • 出力そのもの、出力を加工した情報
      • 前段階の学習に人の手が介在することになるので、ふさわしくない
      • end-to-endが理想的
    • 連続性のないデータ
    • 無意味な数が割り当てられているデータ
  • 欠損値の扱い
    • ゼロで詰める
    • 欠損値を含む集合を除外(行を除外)
    • 入力として採用しない(列を除外)
  • データの結合
  • 数値の正規化・正則化

過学習

  • 巨大なNNで発生しやすい
  • テストデータの誤差が小さくならない
  • 予防策：ドロップアウト

エピローグ

データ集合の拡張

  • 学習データが不足するときに、人工的にデータを作り水増しする
  • 分類タスク(画像認識)に効果が高い
    • 様々な増やし方がある
      • オフセット、ノイズ、ぼかし、回転、クロップなど
    • 様々な変換を組み合わせる
  • 密度推定のためのデータは水増し不可
    • 水増しには密度の情報が必要
  • データ拡張の結果、データセット内で混同するデータが発生しないよう要注意

ノイズ注入によるデータ拡張

  • 中間層へのノイズ注入で、様々な抽象化レベルでのデータ拡張が可能

  • データ拡張の効果なのか？モデル性能か？
    • 見極めが重要
  • データ拡張と性能評価
    • 汎化性能が向上(しばしば劇的に)
    • ランダムなデータ拡張では再現性に注意
  • データ拡張とモデルの捉え方
    • 一般的に適用可能なデータ拡張はモデルの一部として捉える
      • 例：ノイズ付加、ドロップアウトなど
    • 特定の作業に対してのみ適用可能なデータ拡張は、入力データの事前加工として捉える
      • 例：判定対象の画像が製品全体の画像であるとき、製品の一部をクロップしたものを学習してもあまり意味がない

CNNで扱えるデータの種類

次元間で繋がりのあるデータを扱える

  1次元 2次元 3次元
単一チャンネル 音声
[時刻、強度]		 フーリエ変換した音声
[時刻、周波数、強度]		 CTスキャン画像
[x, y, z, 強度]
複数チャンネル アニメのスケルトン
[時刻、(腕の値、膝の値…)]		 カラー画像
[x, y, (R, G, B)]		 動画
[時刻、x, y, (R, G, B)]

隣り合うデータが急に変化するのではなく、ある程度ゆるやかに変化する

特徴量の転移

入力データに近い層の特徴量は、色々な画像に応用可能
基本的な特徴量の抽出処理とタスク固有の処理を、別々のパーツに分けることができる
ベースモデル：基本的な学習済みの重み

  • ファインチューニング
    • ベースモデル重みを再学習
  • 転移学習
    • ベースモデルの重みを固定
  基本的な特徴量抽出 タスク固有処理
学習コスト(計算量) 高 低
必要なデータ量 多 少
  VGG(画像)
BERT(テキスト)		 全結合層による分類層

プリトレーニング(基本的な特徴量抽出)がうまくいくと、その分野の学習精度が一気に上がる

実装演習

1_1_forward_propagation.ipynb

順伝播(単層・単ユニット)

  • 配列と数値の初期化方法を変えてみる
    →中間層出力が変化する
    • 例1:
      W = np.array([[0.1], [0.2]]), b = 0.5の場合
      fixed_params
    • 例2:
      W = np.zeros(2), b = np.random.rand()の場合
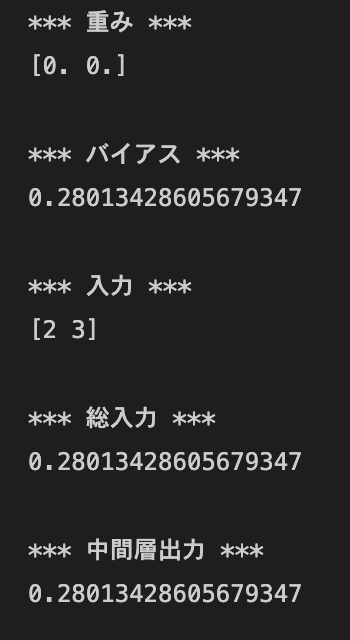
      zeros_rand
    • 例3:
      W = np.random.randint(5, size=(2)), b = np.random.rand * 10 -5の場合
      rand_rand

順伝播(単層・複数ユニット)

  • 配列の初期化方法を変えてみる
    • 例1:
      W = np.ones([4, 3])の場合
      ones
    • 例2:
      W = np.random.rand(4, 3)の場合
      rand

順伝播(3層・複数ユニット)

  • デフォルトの実行結果:
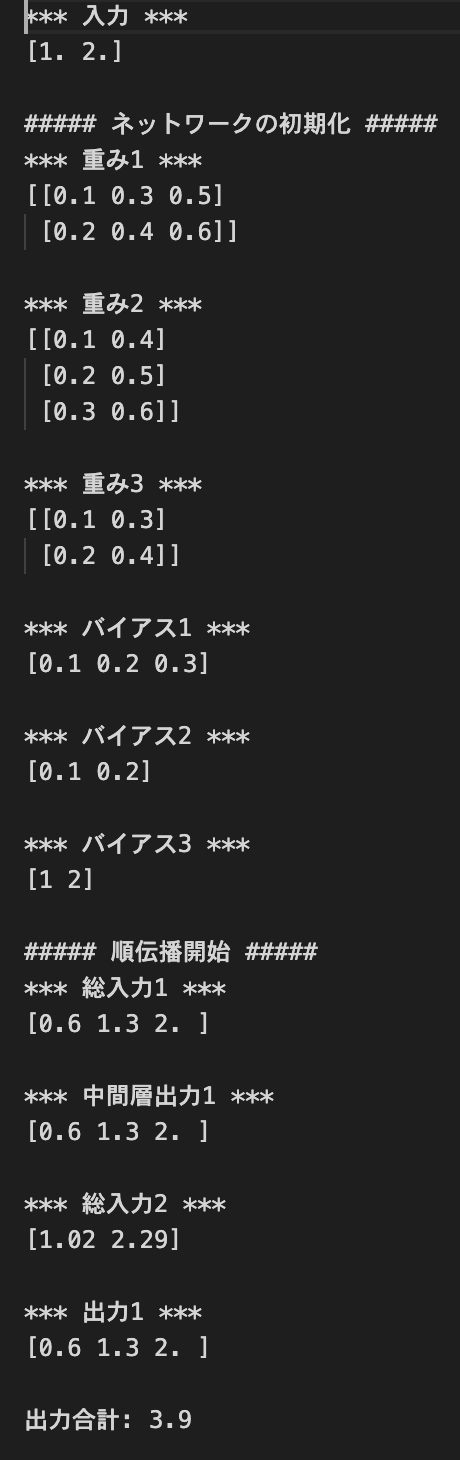
    default
  • 各パラメータのshapeを表示してみる
    • コード:
      code
    • 結果:
      result
  • ネットワークの初期値をランダム生成してみる
    • コード:
      code
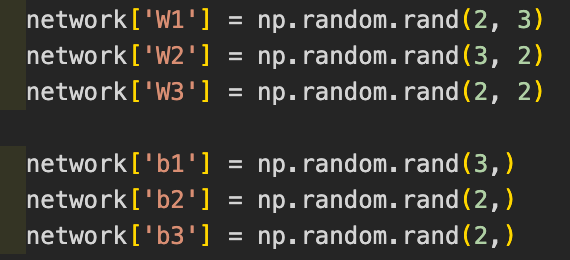
    • 結果:
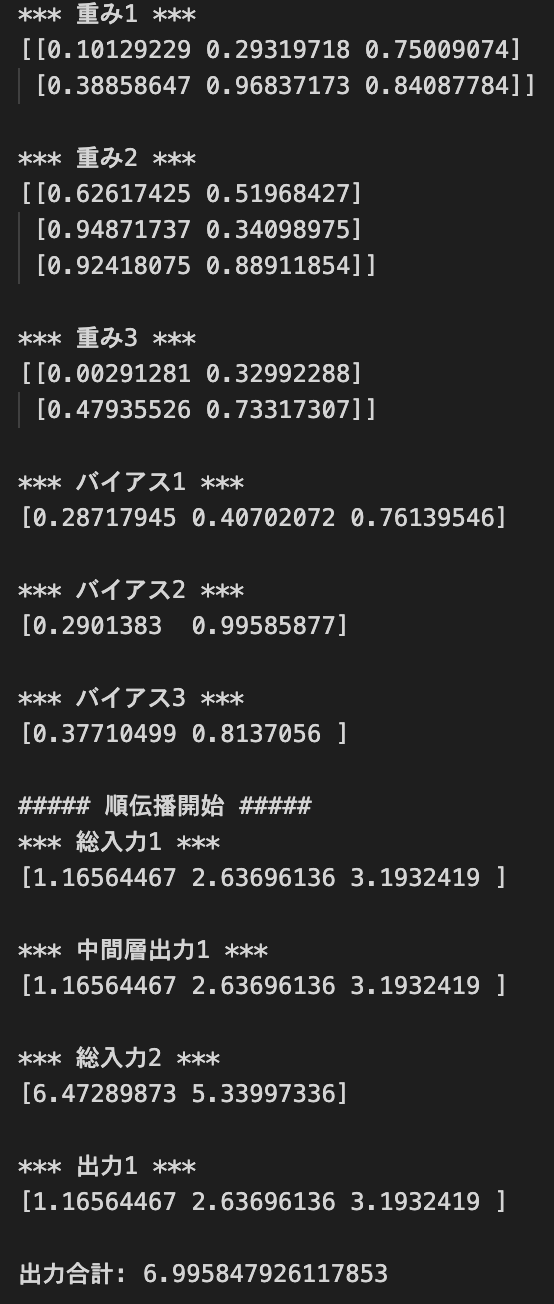
      result

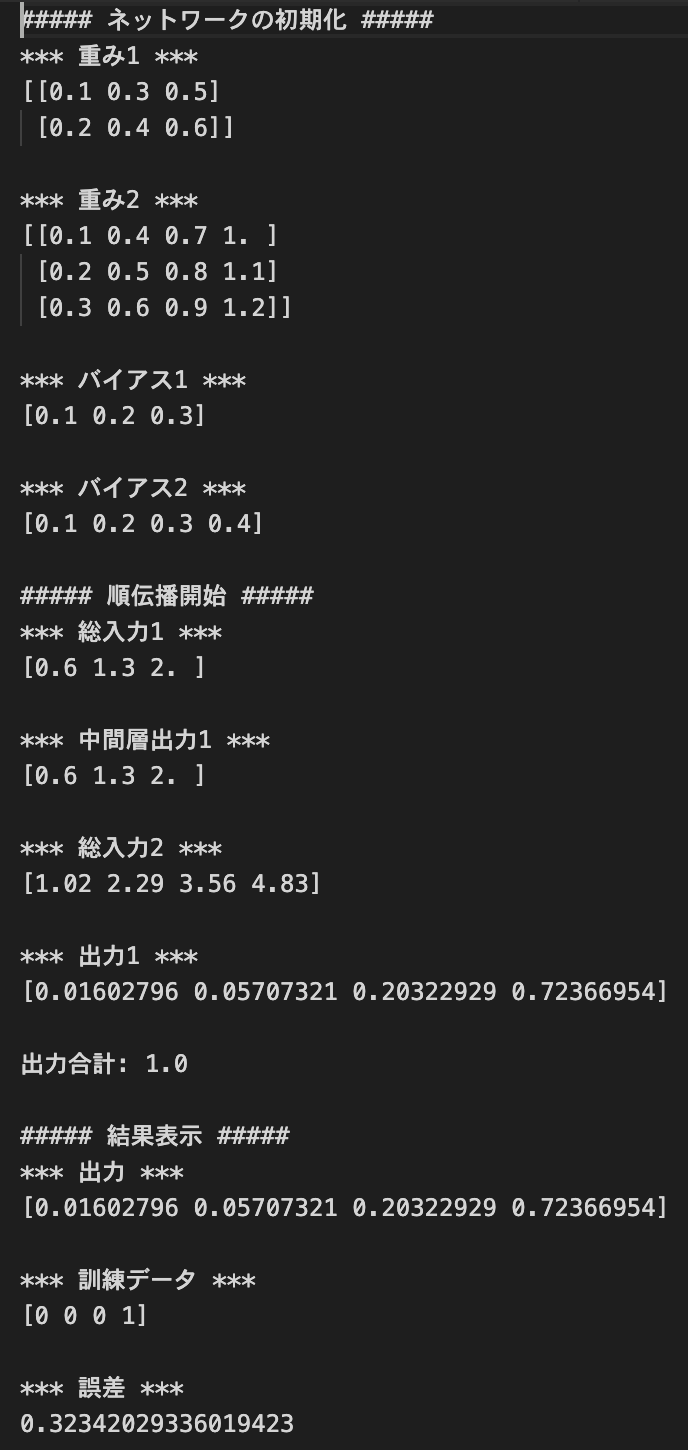
多クラス分類 (2-3-4ネットワーク)

  • デフォルトの実行結果:
    default
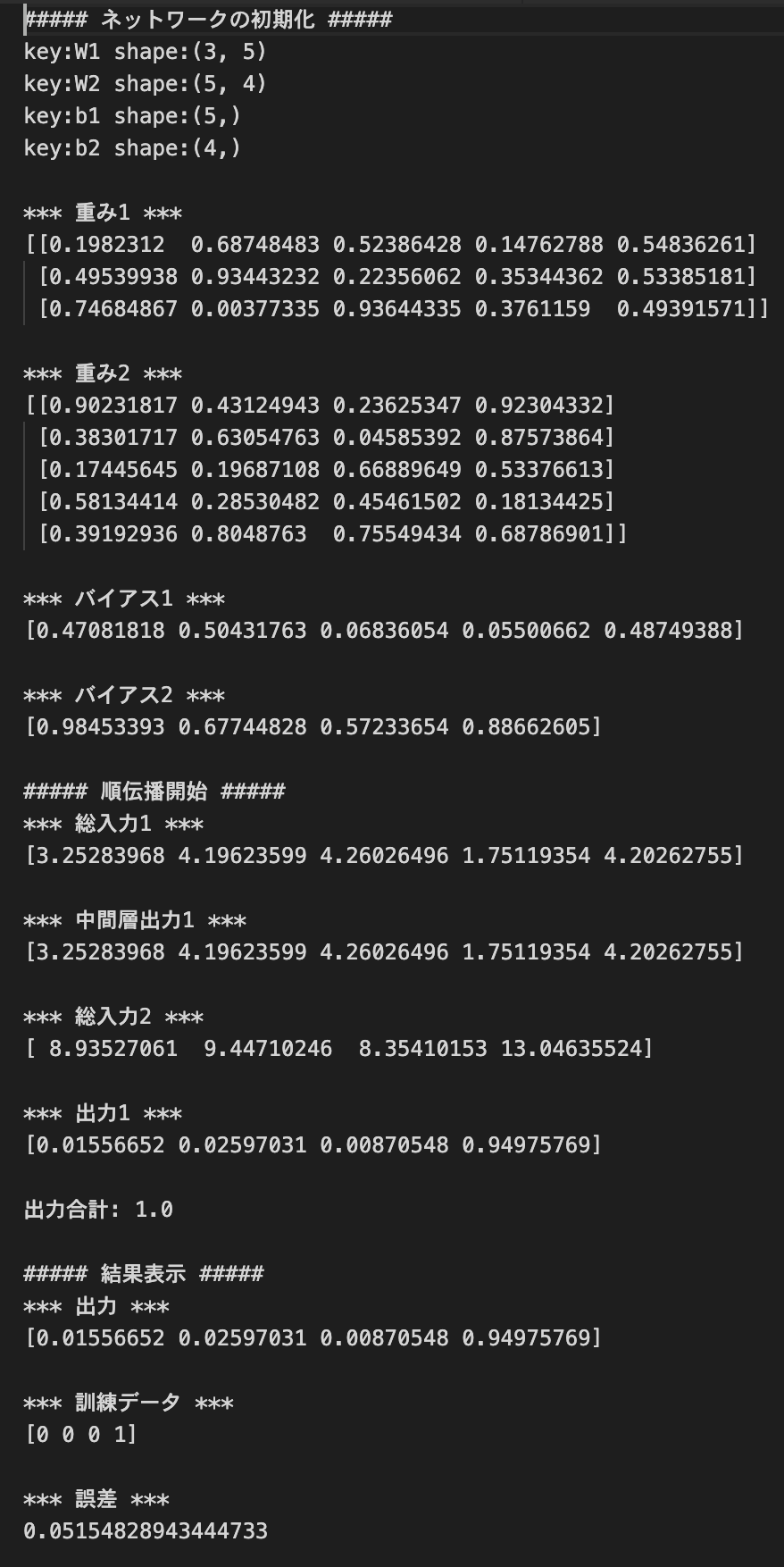
  • ノードの構成を変えてみる 2-3-4 → 3-5-4
    • コード:
      • ネットワークの初期化
        code1
      • 入力値
        code2
    • 結果:
      result

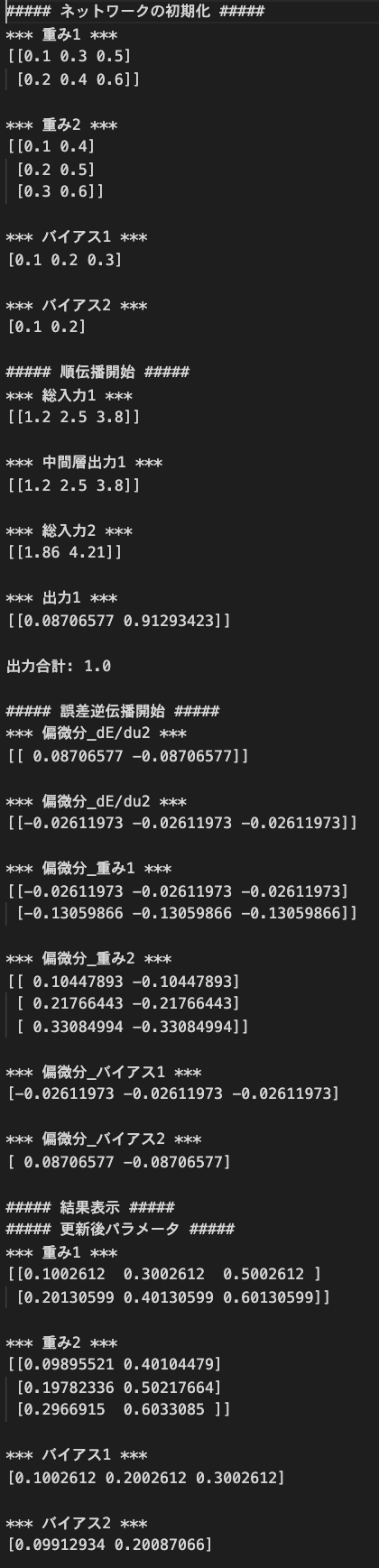
1_2_back_propagation.ipynb

逆誤差伝播を行う
実行結果：
result_bp

1_3_stochastic_gradient_descent.ipynb

  • デフォルトの実行結果：
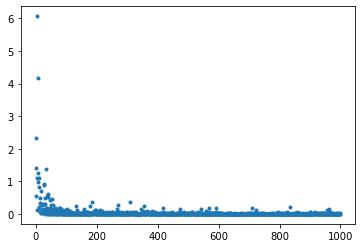
    default
  • 確率的勾配降下法
    • 以下を試す
      try
      • 結果：わずかにデータのばらつきが大きくなった
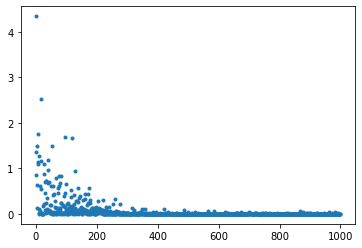
        result
    • 上記をそのままにして、以下も試す
      try2
      • 結果：データのばらつきがかなり大きくなった
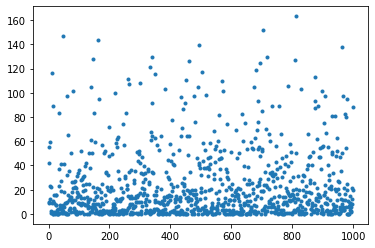
        result2

1_4_1_mnist_sample.ipynb

  • デフォルトの実行結果：
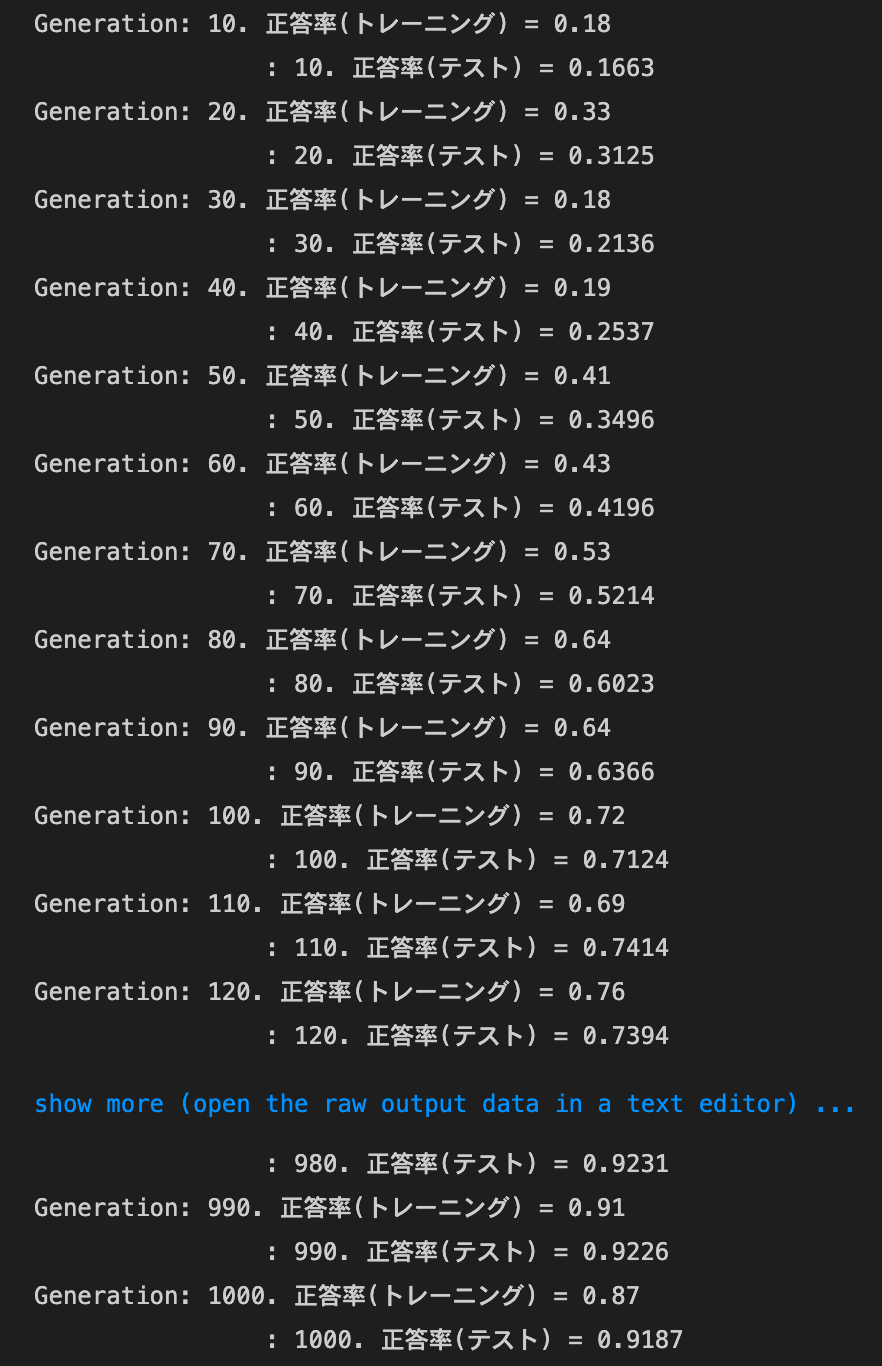
    default
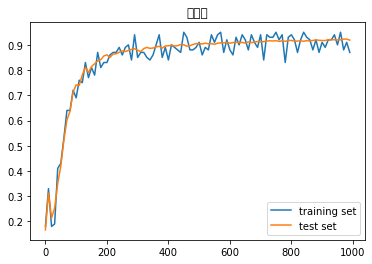
    default_graph
    • Xavierの初期値を試す
      Xavier
      • 結果：training setの正答率のばらつきが大きくなり、test setの正答率は上がった
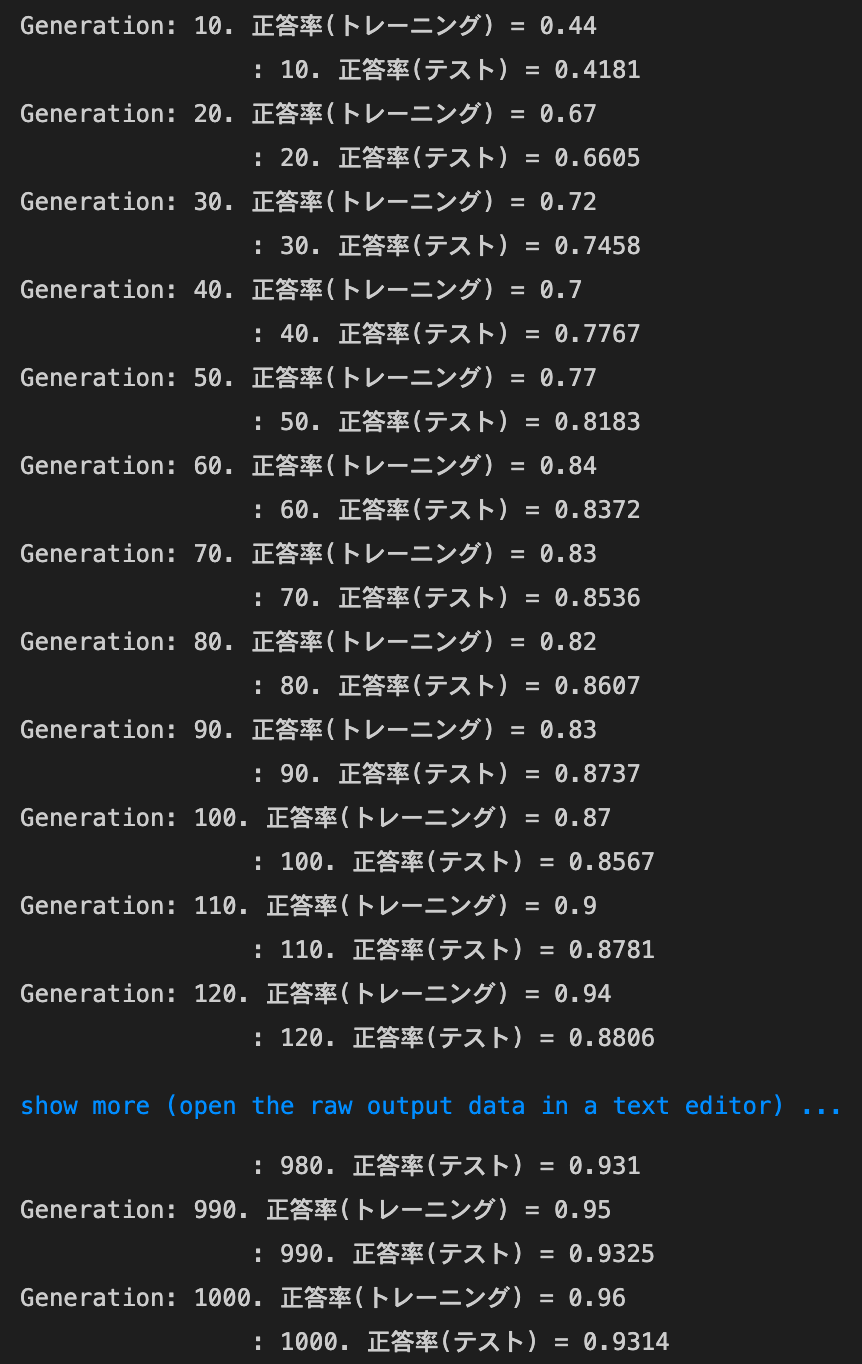
        result
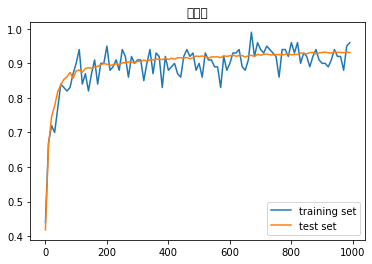
        graph
    • Heの初期値を試す
      He
      • 結果：Xavierとほぼ同様の変化があった
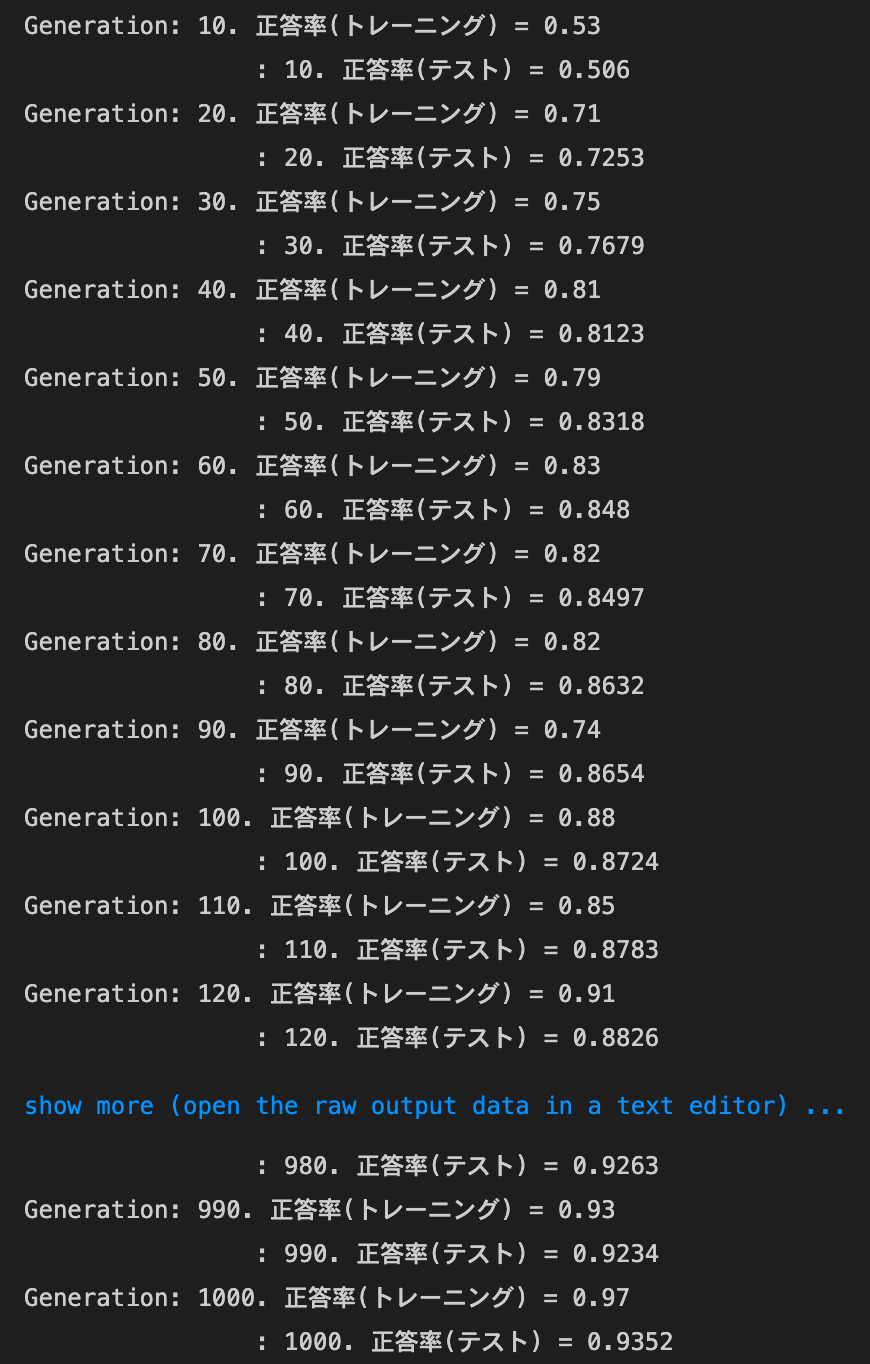
        result
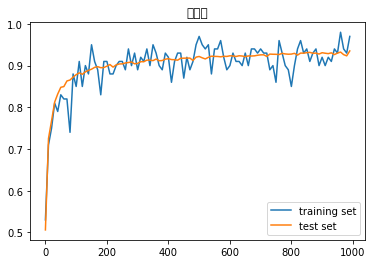
        graph