【ラビット・チャレンジ】深層学習 前編 Day2
【目次】
- 深層モデルのための学習テクニック
- 畳み込みニューラルネットワークについて
- 実装演習
ラビット・チャレンジの受講レポート。
深層モデルのための学習テクニック
勾配消失問題について
誤差逆伝播法が下位層へ進んでいくにつれ、勾配が緩やかになっていく
→勾配降下法による更新では、下位層のパラメータがほとんど変わらず、
訓練は最適解に収束しなくなる
確認テスト
連鎖律の原理を使い、dz / dxを求めよ
\[z = t^2 \\ t = x + y\]解答:
\[\begin{split} \frac{dz}{dx} &= \frac{dt}{dx} \cdot \frac{dz}{dt} \\ \frac{dt}{dx} & = 1 \\ \frac{dz}{dt} &= 2t \\ \frac{dz}{dx} &= 2t \\ &= 2(x + y) \end{split}\]- シグモイド関数
- 勾配消失問題を起こしやすい
- 微分すると最大0.25
確認テスト1
シグモイド関数を微分したとき、入力値が0のときに最大値をとる
その値として正しいのは?
【答え】0.25
勾配消失の解決方法:
- 活性化関数の選択
- 重みの初期値設定
- バッチ正規化
活性化関数
-
ReLU関数
\[f(x) = \left\{ \begin{array}{ll} x & (x > 0) \\ 0 & (x \leqq 0) \\ \end{array} \right.\]# サンプルコード def relu(x): return np.maximum(0, x)- 微分結果が1か0になる
- 勾配消失問題の回避
- スパース化
- 必要な部分だけ使用し、あまり役立たない部分は切り捨てられる
- 微分結果が1か0になる
- ソフトマックス
- tanh(ハイパボリックタンジェント)
- Leaky ReLU
初期値の設定方法
重みに乱数を使う理由:
入力に対していろんな見方をしたいため
どういう見方をしたらうまくいくか?を求めたい
- Xavier
- Xavierの初期値を設定する際の活性化関数
- ReLU
- シグモイド(ロジスティック関数)
- 双曲線正接関数
- →S字カーブ型の関数に対してうまくはたらく
- 初期値の設定方法
- 重みの要素を、前の層のノード数の平方根で除算した値
# サンプルコード:Xavierの初期値 network['W1'] = np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size) network['W2'] = np.random.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size)- Xavierがよい理由
- 当初は標準正規分布がよく用いられたが、逆誤差伝播法で勾配消失問題が発生する
- →標準正規分布で重みを初期化したとき、各レイヤーの出力は0と1に偏る
- →0や1のときは微分値がほとんど0
- →標準偏差を小さくする(例:0.01)と、出力値のほとんどが0.5近辺になる
- →Xavierを使うと出力値の分布がいい感じにばらける
- Xavierの初期値を設定する際の活性化関数
- He(ヒー)
- Heの初期値を設定する際の活性化関数
- ReLU関数
- 初期化の設定方法
- 重みの要素を、前の層のノード数の平方根で除算した値に対し、$\sqrt{2}$をかけ合わせた値
- = 正規分布の重みを$\sqrt{\frac{2}{n}}$の標準偏差の分布にする($n$は前の層のノード数)
- 重みの要素を、前の層のノード数の平方根で除算した値に対し、$\sqrt{2}$をかけ合わせた値
# サンプルコード:Heの初期値 network['W1'] = np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size) * sqrt(2) network['W2'] = np.random.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size) * sqrt(2)- Heがよい理由
- 標準正規分布に基づいた重みを用いてReLU関数を通すと表現力が全くなくなる(ほとんど0)
- →標準偏差を小さくしても、表現力はなくなっていく
- →He初期化すると、0 ~ 1の範囲の分布が増える
- Heの初期値を設定する際の活性化関数
確認テスト
重みの初期値に0を設定すると、どのような問題が発生するか?
【解答】
正しい学習が行われない
→全ての重みの値が均一に更新されるため
多数の重みをもつ意味がなくなる
バッチ正規化
ミニバッチ単位で、入力値のデータの偏りを抑制する手法
- 使い所
- 活性化関数へ値を渡す前後に、バッチ正規化の処理を孕んだ層を加える
- バッチ正規化層への入力
- $u^{(l)} = w^{(l)} z^{(l-1)} + b^{(l)}$
- または$z$
- バッチ正規化層への入力
- 活性化関数へ値を渡す前後に、バッチ正規化の処理を孕んだ層を加える
- ミニバッチのサイズ(画像の場合)
- GPUの場合:1 ~ 64枚
- TPUの場合:1 ~ 256枚
- 小さい分には問題ない
- 8(または2)の倍数にすることが多い
- ハードウェアの制限のため
- メリット
- NNの学習が安定化、スピードアップ
- 過学習を抑制
-
数学的記述
\[\begin{array}{ll} 1. \quad \mu_t = \frac{1}{N_t} \sum_{i=1}^{N_t} x_{ni} & : ミニバッチの平均 \\ 2. \quad \sigma_t^2 = \frac{1}{N_t} \sum_{i=1}^{N_t} (x_{ni} - \mu_t)^2 & : ミニバッチの分散 \\ 3. \quad \hat x_{ni} = \frac{x_{ni} - \mu_t}{\sqrt{\sigma_t^2 + \theta}} & : ミニバッチの正規化 \\ 4. \quad y_{ni} = \gamma x_{ni} + \beta & : 変倍・移動 \end{array}\](1. ~ 3.は統計的正規化、4.はNNでの扱いを良くするための調整)
- 処理および記号の説明
- $\mu_t$: ミニバッチ$t$全体の平均
- $\sigma_t^2$: ミニバッチ$t$全体の標準偏差
- $N_t$: ミニバッチのインデックス
- $\hat x_{ni}$: 0に値を近づける計算(0を中心とするセンタリング)と正規化を施した値
- $\gamma$: スケーリングパラメータ
- $\beta$: シフトパラメータ
- $y_{ni}$: ミニバッチのインデックス値とスケーリングの積にシフトを加算した値
(バッチ正規化オペレーションの出力)
- 処理および記号の説明
確認テスト
一般的に考えられるバッチ正規化の効果を2点挙げよ
- NNの学習が安定化、スピードアップ
- 過学習を抑制
例題チャレンジ
特徴データdata_x, ラベルデータdata_tに対してミニバッチ学習を行うプログラム
空欄(き)に当てはまるものは?
【解答】
data_x[i:i_end], data_t[i:i_end]
→バッチサイズだけデータを取り出す処理
E資格ではプログラムの穴埋め問題がよく出る
学習率最適化手法について
学習率の決め方
初期の指針
- 初期は大きく、徐々に小さくしていく
- パラメータごとに学習率を可変
→学習率最適化手法を利用して学習率を最適化
モメンタム
誤差をパラメータで微分したものと学習率の積を減算した後、
現在の重みに前回の重みを減算した値と慣性の積を加算
株価の移動平均のような、なめらかな動きをする
- 慣性:$\mu$
- Vには基本的にwと同じ値が入る(意味合いが異なる)
self.v[key] = self.momentum * self.v[key] - self.learning_rate * grad[key]
params[key] += self.v[key]
- コード上の各変数の意味
self.momentum: $\mu$self.learning_rate: $\epsilon$self.grad[key]: $\nabla E$
- メリット
- 局所的最適解にはならず、大域的最適解となる
- 谷間についてから最も低い位置(最適値)にいくまでの時間が早い
AdaGrad
誤差をパラメータで微分したものと
再定義した学習率の積を減算する
self.h[key] = np.zeros_like(val)
self.h[key] += grad[key] * grad[key]
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)
- コード上の各変数の意味
val: $\theta$1e-7: 2個目の$\theta$- 計算がうまくいくように、適当な値を足している
- メリット
- 勾配の緩やかな斜面に対して、最適解に近づける
- 課題
- 学習率が徐々に小さくなるので、鞍点問題を引き起こすことがあった
RMSProp
AdaGradの改良版、似たような動きをする
誤差をパラメータで微分したものと
再定義した学習率の積減算する
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grad[key] * grad[key]
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)
- コード上の各変数の意味
self.decay_rate: $\alpha$
- メリット
- 局所的最適解にはならず、大域的最適解となる
- ハイパーパラメータの調整が必要な場合が少ない
Adam
以下をそれぞれ孕んだ最適化アルゴリズム
- モメンタムの、過去の勾配の指数関数的減衰平均
-
RMSPropも、過去の勾配の2乗の指数関数的減衰平均
- メリット
- モメンタムとRMSPropのメリットを孕む
- 鞍点問題もクリアしやすい
- スムーズに学習が進む
過学習
テスト誤差と訓練誤差とで学習曲線が乖離がすること
ネットワークの自由度が高いと起こりやすい
- 入力値:少、NN:大
- パラメータ数が適切でない
- など
L1正則化、L2正則化
ネットワークの自由度を制約する
→過学習を防ぐ
【Weight decay(荷重減衰)】
- 過学習の原因:重みが大きい値をとる(と、過学習が発生することがある)
- 過学習の解決策:誤差に対して正則化項を加算することで、重みを抑制
【数式】
\[\begin{array}{ll} E_n(w) + \frac{1}{p} \overbrace{\lambda}^{hyper \space parameter} || x ||_p & : 誤差関数に、pノルムを加える \\ || x ||_p = \Bigl( |x_1|^p + \cdots + |x_n|^p \Bigr)^{\frac{1}{p}} & : pノルムの計算 \end{array}\]- L1正則化:$p = 1$の場合。Lasso回帰
- L2正則化:$p = 2$の場合。Ridge回帰
ノルム=距離
例:
点(x, 0)から点(0, y)までの距離
- ユークリッド距離:$\sqrt{x^2 + y^2} \quad$ ←p2ノルム
- マンハッタン距離:$x + y \quad \quad \quad$ ←p1ノルム
【正則化の計算】
\[\begin{split} &||W^{(1)}||_p = (|W_1^{(1)}|^p + \cdots + |W_n^{(1)}|^p)^{\frac{1}{p}} \\ &||W^{(2)}||_p = (|W_1^{(2)}|^p + \cdots + |W_n^{(2)}|^p)^{\frac{1}{p}} \\ &||x||_p = ||W^{(1)}||_p + ||W^{(2)}||_p \\ &E_n(w) + \underbrace{\frac{1}{p} \lambda ||x||_p}_{正則化項} \end{split}\]# サンプルコード
np.sum(np.abs(network.params['W' + str(idx)]))
weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, b_batch) + weight_decay
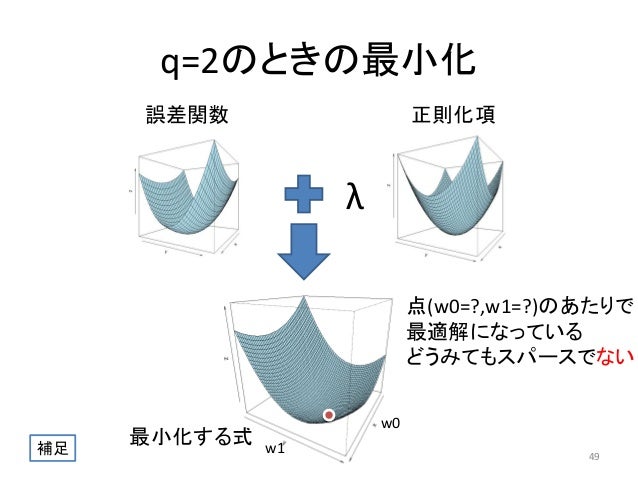
(画像:https://www.slideshare.net/yasunoriozaki12/prml-29439402)
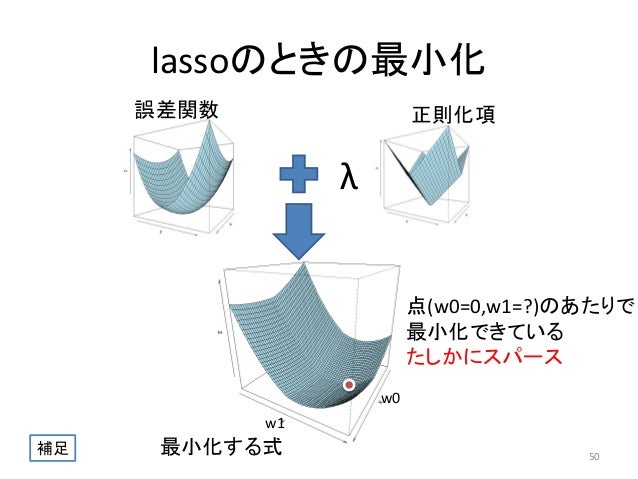
(画像:https://www.slideshare.net/yasunoriozaki12/prml-29439402)
→スパース化(ReLU関数のときのように)
確認テスト
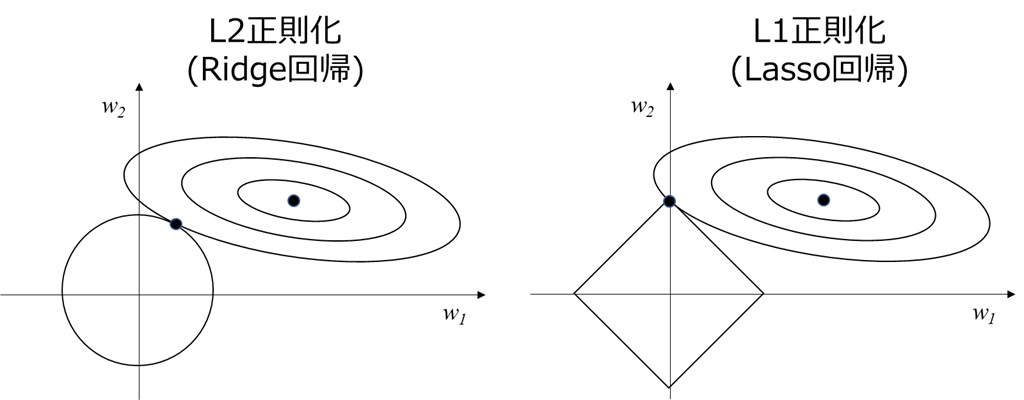
L1正則化を表しているグラフは?
【解答】右(Lasso推定量)
(画像:https://qiita.com/c60evaporator/items/784f0640004be4eefc51)
この図の意味:上の3Dグラフを上から見て、等高線を引いた感じ
- 右上の同心楕円:誤差関数の等高線
- L2の円、L1の正方形(左下):正則化項の等高線
- 同心楕円と左下の[円 / 正方形]の交点:誤差関数と正則化項の最小値
- 誤差関数の最小値:同心楕円の中心
- 正則化項の最小値:[円 / 正方形]の中心
L1正則化では、$w1$方向の重みが0になる
例題チャレンジ
- パラメータ正則化
- L2正則化の最終的な勾配を計算するコードは?
grad += rate * param- ↑「勾配」なので微分した結果
- L1正則化の最終的な勾配を計算するコードは?
x = np.sign(param)- ↑あるパラメータに着目。0未満の傾きは-1, 0以上の傾きは1
- L2正則化の最終的な勾配を計算するコードは?
ドロップアウト
ランダムにノードを削除して学習させる
メリット:
データ量を変化させずに、異なるモデルを学習させていると解釈できる
→過学習の抑制につながる
畳み込みニューラルネットワークについて
畳み込みニューラルネットワークの概念
次元間で繋がりのあるデータを扱える
例:LeNetの構造図

(画像:https://buildersbox.corp-sansan.com/entry/2020/02/28/110000)
データの数の変化
(32, 32) -> (28, 28, 6) -> (14, 14, 6) -> (10, 10, 16) -> (5, 5, 16) -> (120,) -> (84,) -> (10,)
- 前半部分(〜S4の層)
- 次元のつながりを保つ
- 特徴量の抽出
- 後半部分(C5〜の層)
- 全結合層
- 人間が欲しい結果を出す
- フィルタについて
- 例:C1の層では、6種類のフィルタを使って学習する
【畳み込み層】
(入力値) * (フィルター) → (出力値) + (バイアス) → (活性化関数) → (出力値)
$\Rightarrow$データの繋がりを反映させることができる
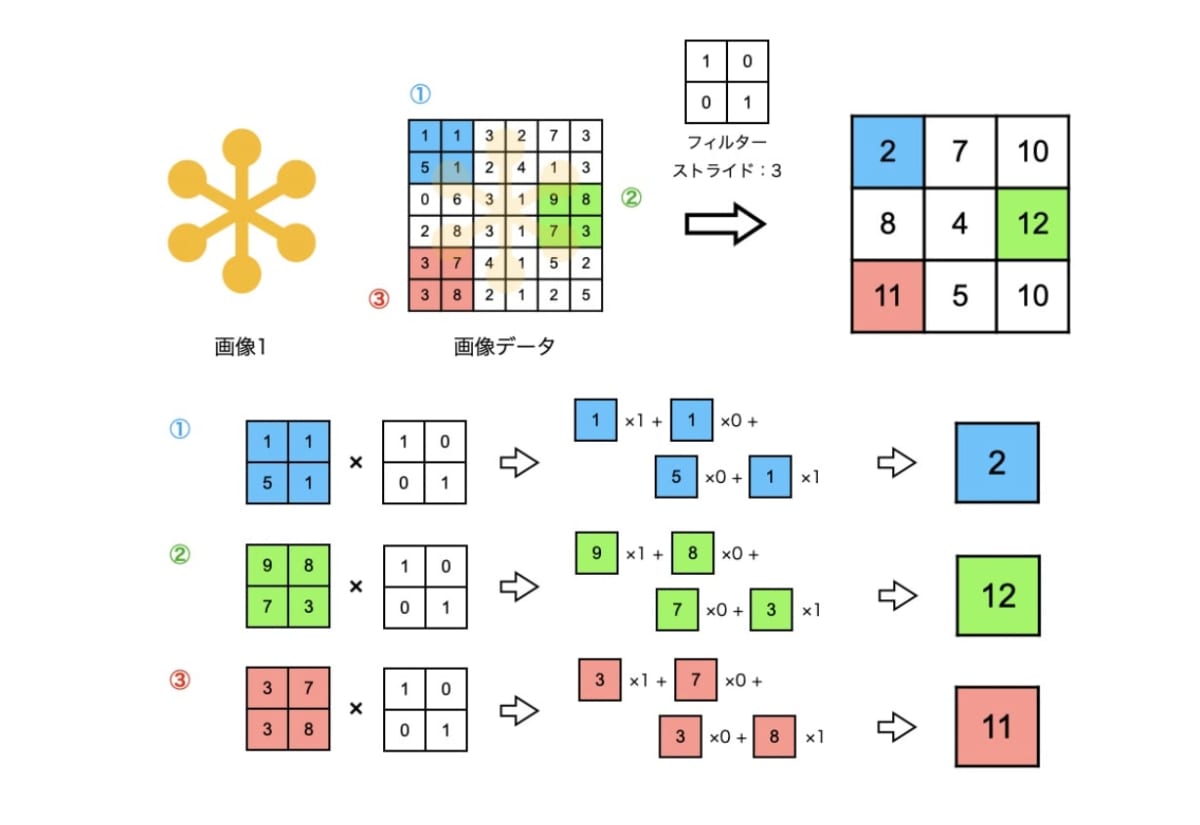
[計算方法のイメージ]
フィルターを左上から一定間隔ずつずらしながら、出力値を計算していく
フィルター:重み
(画像:https://ainow.ai/2021/09/16/258469/)
畳み込み層
3次元の空間情報も学習できる
- 全結合層のデメリット
- 画像の場合3次元データだが(w * h * ch)、1次元のデータとして処理される
- →RGBの各チャンネル間の関連性が、学習へ反映されない
- 画像の場合3次元データだが(w * h * ch)、1次元のデータとして処理される
畳み込み層ではこの問題が解決される
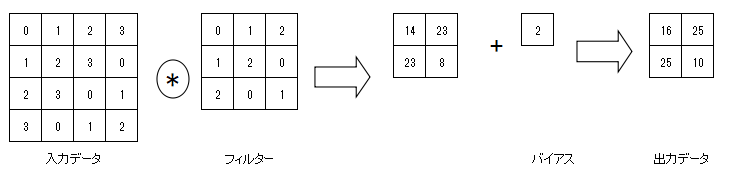
【バイアス】
(入力値) * (フィルター)の値へ足す
$xW + \underbrace{b}_{バイアス}$
(画像:https://qiita.com/nvtomo1029/items/601af18f82d8ffab551e)
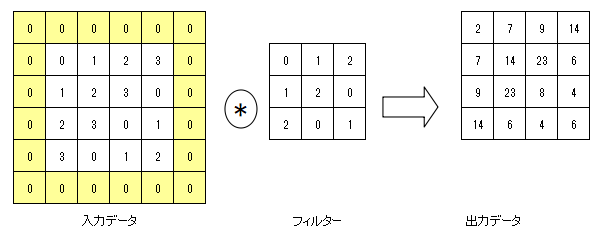
【パディング】
出力データのサイズが小さくなることを防ぐために、入力データの周りにデータを足す
(以下の画像の例では0にしているが、0以外でもよい。一番近い値など)
(画像:https://qiita.com/nvtomo1029/items/601af18f82d8ffab551e)
【ストライド】
フィルタを一度にずらす幅
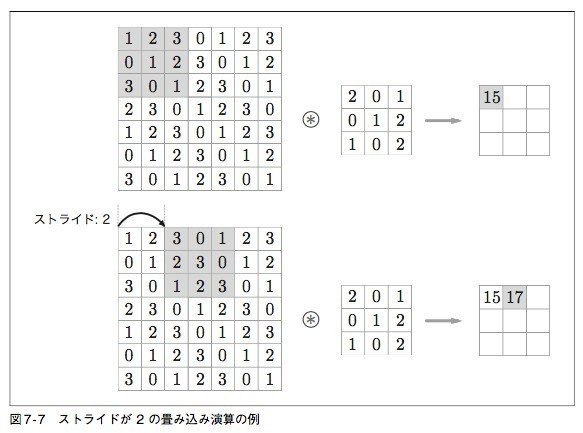
(画像:https://note.com/ryuwryyy/n/nfd0b8ff862aa)
【チャンネル】
フィルタの数
以下の画像の例では3
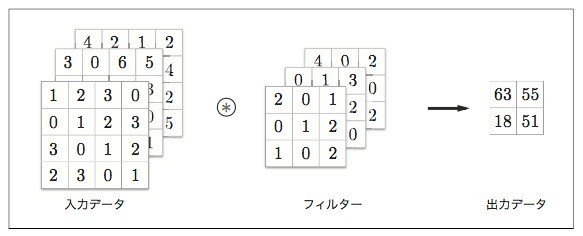
(画像:https://note.com/ryuwryyy/n/nfd0b8ff862aa)
プログラム上では、計算を高速化するために入力データの行列を変形させてから計算する
例えば以下のような行列があったら、

(画像:https://medium.com/@_init_/an-illustrated-explanation-of-performing-2d-convolutions-using-matrix-multiplications-1e8de8cd2544)
以下のように変形する

(画像:https://medium.com/@_init_/an-illustrated-explanation-of-performing-2d-convolutions-using-matrix-multiplications-1e8de8cd2544)
→重みの行列との計算が簡単にできる形になる
プーリング層
- Max Pooling: 対象領域のMax値を取得
- Avg. Pooling: 対象領域の平均値を取得
この層に重みはない
確認テスト
サイズ6 * 6の入力画像を、サイズ2 * 2のフィルタで畳み込んだときの出力画像のサイズは?
なお、ストライドとパディングは1とする
【解答】6 * 6
公式
\[\begin{split} &O_H = \frac{画像の高さ + 2 * パディング高さ - フィルター高さ}{ストライド} + 1 \\ &\space \\ &O_W = \frac{画像の幅 + 2 * パディング幅 - フィルター幅}{ストライド} + 1 \end{split}\]初期のCNN
AlexNet
5層の畳み込み層及びプーリング層など、それに続く3層の全結合層から構成される
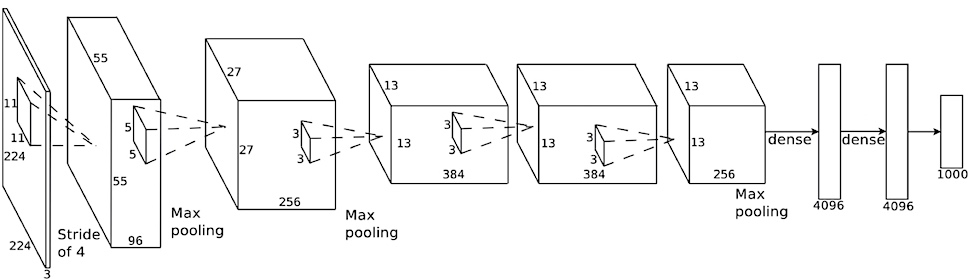
(画像:https://ml4a.github.io/ml4a/jp/convnets/)
過学習の防止 →サイズ4096の全結合層の出力にドロップアウトを使用
【全結合層への変換方法】
- Flatten: データの形状をベクトルに変換する(1列に並べ替える)
- 上図の場合は43,264個のデータになる
- Global Max Pooling: 各レイヤーで一番大きいものを選ぶ
- 上図の場合は256個のデータになる
- Global Avg Pooling: 各レイヤーの平均を使う
- 上図の場合は256個のデータになる
Global Max PoolingやGlobal Avg Poolingの方が精度が高い
実装演習
2_1_network_modified.ipynb
1_4_1_mnist_sample.ipynbの改良版
実行結果:
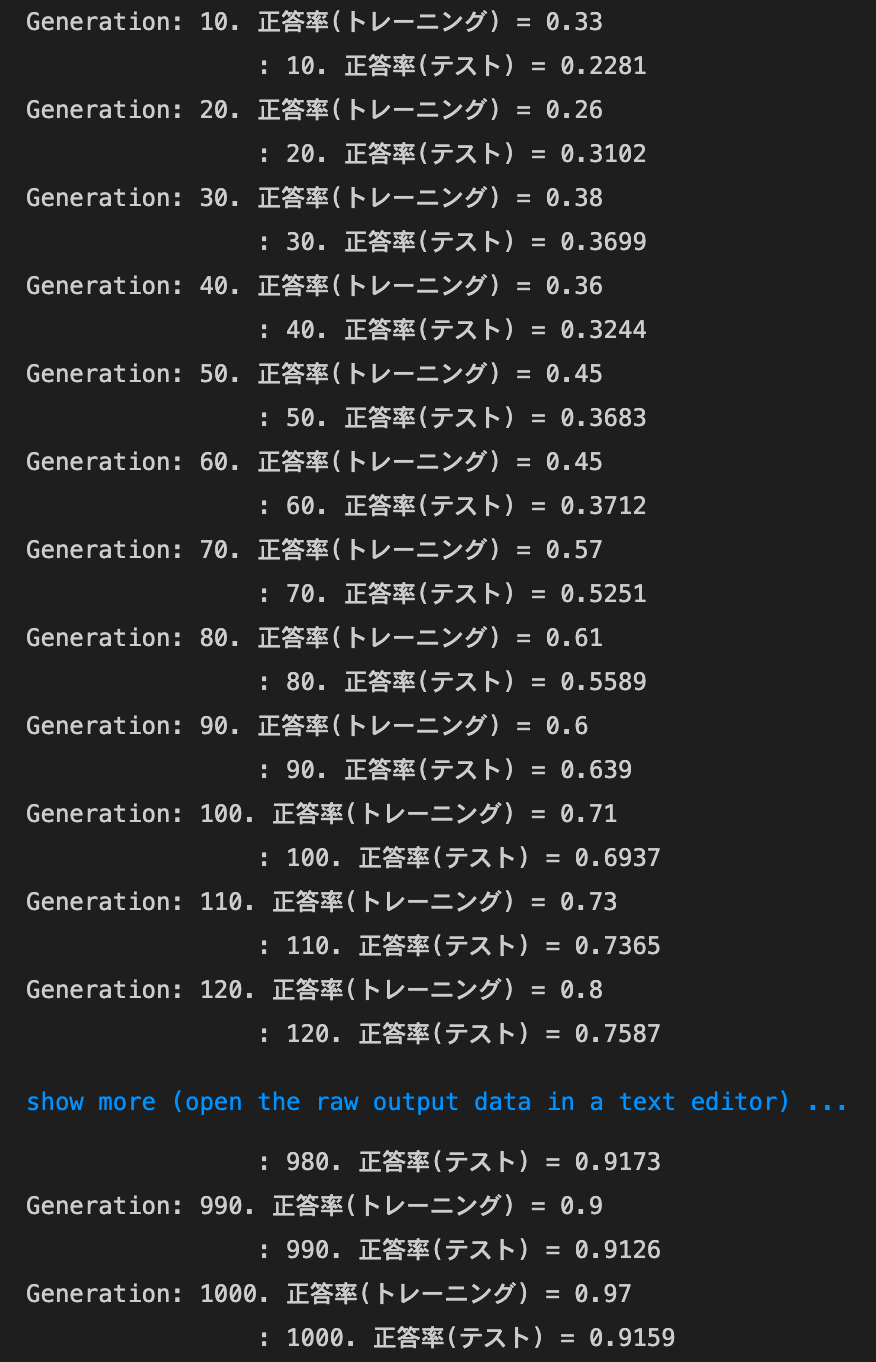
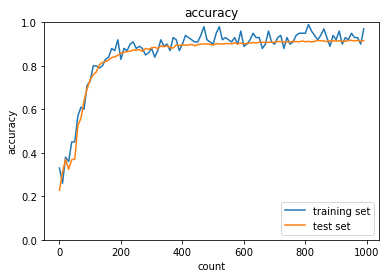
2_2_2_vanishing_gradient_modified.ipynb
sigmoid - gauss
実行結果:
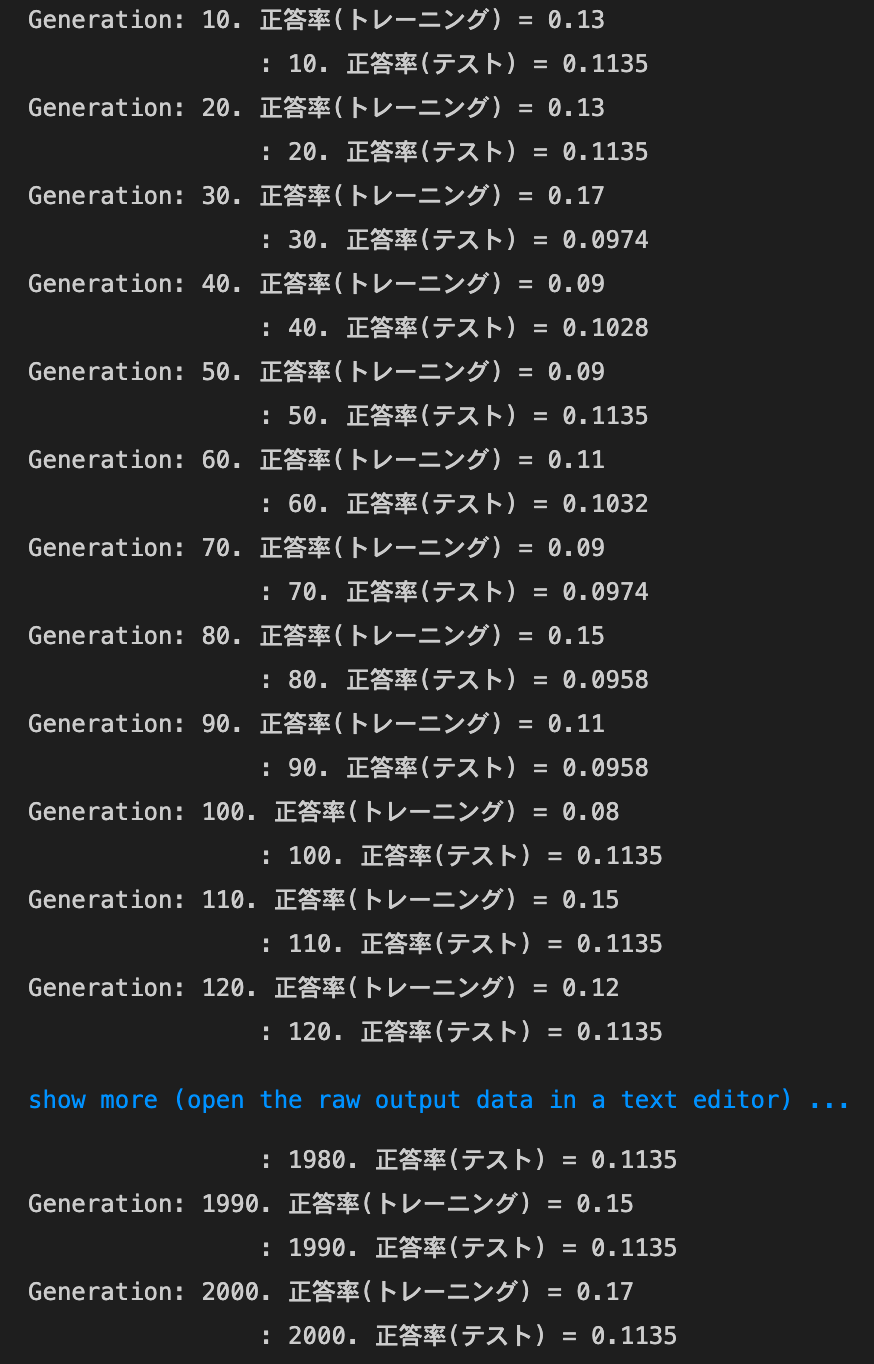
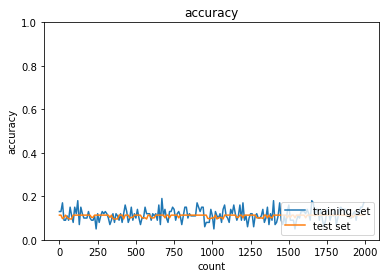
ReLU - gauss
実行結果:
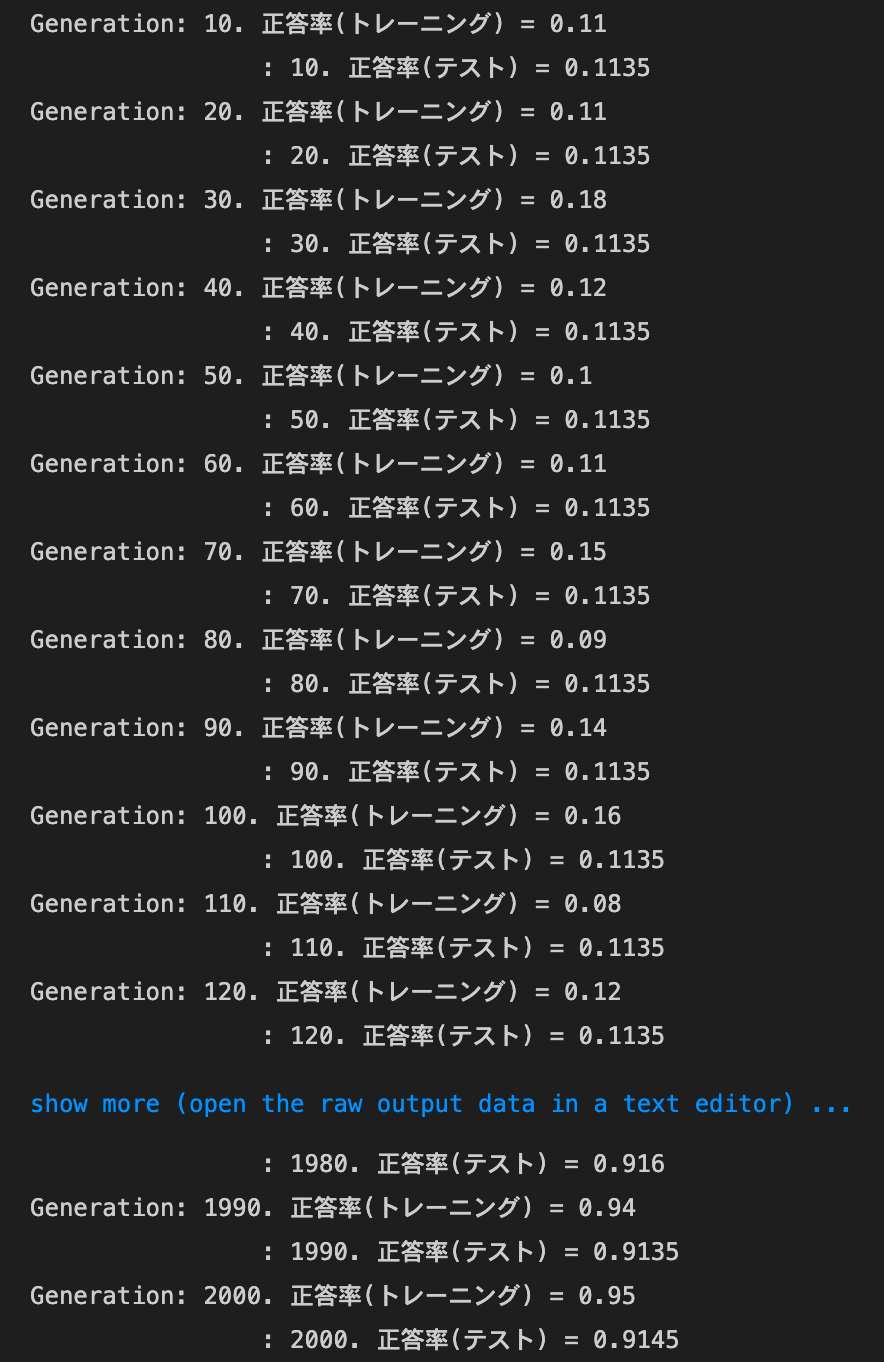
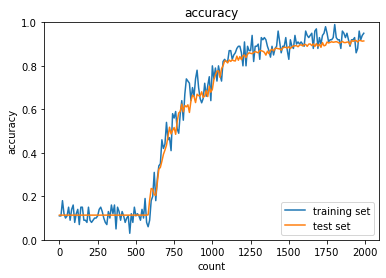
sigmoid - Xavier
実行結果:
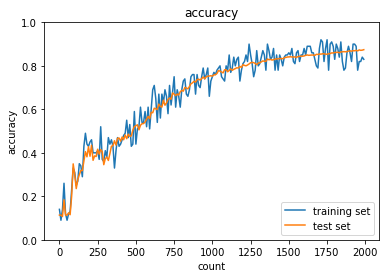
ReLU - He
実行結果:
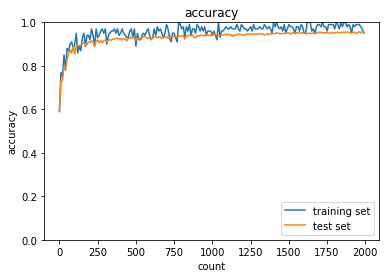
- [try]
hidden_size_listの数字を変更してみる[40, 20]から[1000, 500]に変更したところ、全ての方法で精度が上がり、
試行回数が比較的少ないうちから精度が上がるようになったsigmoid - gaussの正答率:- トレーニング:0.17 → 0.68
- テスト:0.1135 → 0.6654

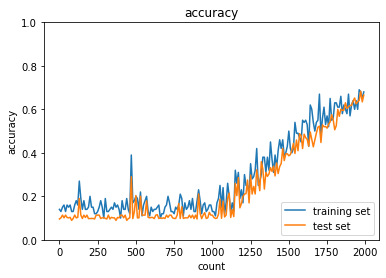
ReLU - gaussの正答率:- トレーニング:0.95 → 0.99
- テスト:0.9145 → 0.9584

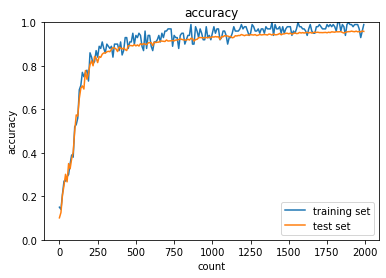
sigmoid - Xavierの正答率:- トレーニング:0.83 → 0.87
- テスト:0.8744 → 0.8998

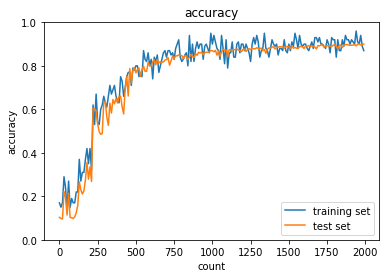
ReLU - Heの正答率:- トレーニング:0.95 → 1.0
- テスト:0.9548 → 0.9701

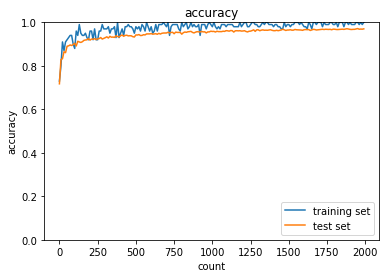
[40, 20]から[10, 5]に変更したところ、ほぼ全ての方法で精度が下がり、
試行回数が比較的多くならないと精度が上がらなくなったsigmoid - gaussの正答率:- トレーニング:0.17 → 0.11
- テスト:0.1135 → 0.1135

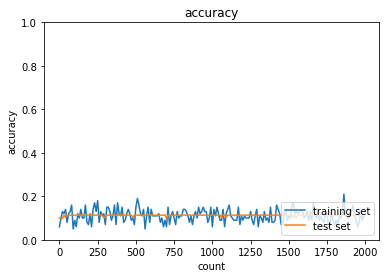
ReLU - gaussの正答率:- トレーニング:0.95 → 0.74
- テスト:0.9145 → 0.7329

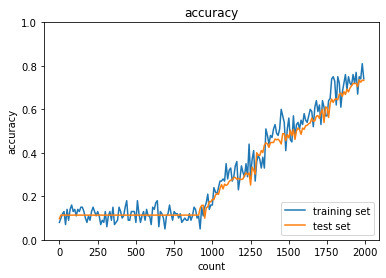
sigmoid - Xavierの正答率:- トレーニング:0.83 → 0.79
- テスト:0.8744 → 0.7587

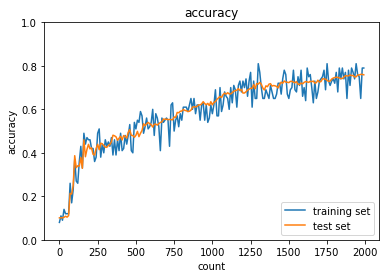
ReLU - Heの正答率:- トレーニング:0.95 → 0.95
- テスト:0.9548 → 0.892

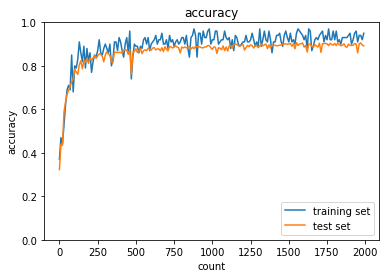
- [try]
sigmoid - HeとReLU - Xavierについても試してみるsigmoid - Henetworkの初期化処理を、以下のようにしたhidden_size_list = [40, 20] network = MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='sigmoid', weight_init_std='He')- 結果:
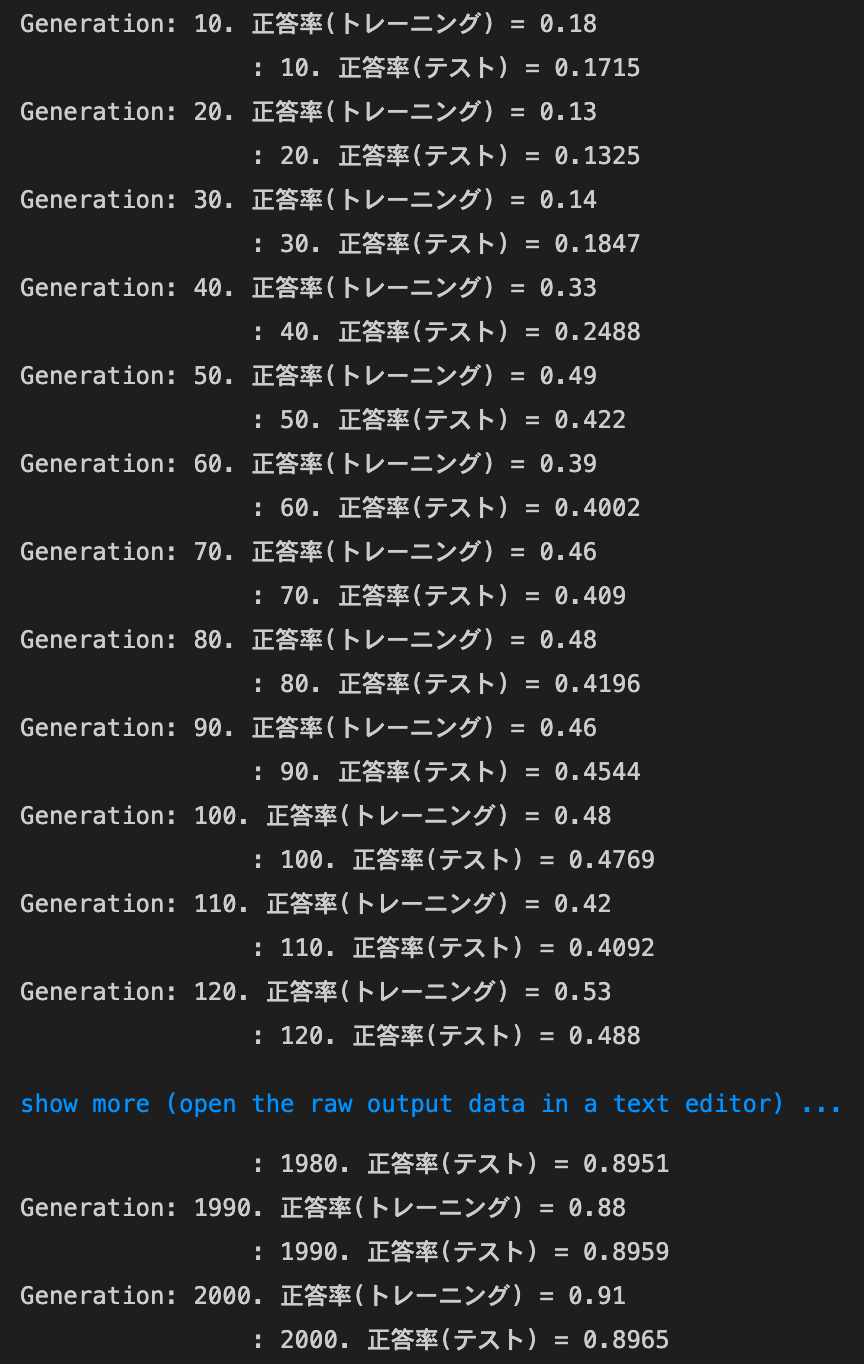
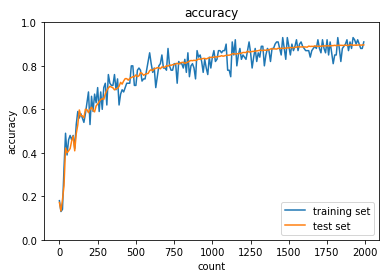
ReLU - Xaviernetworkの初期化処理を、以下のようにしたhidden_size_list = [40, 20] network = MultiLayerNet(input_size=784, hidden_size_list=hidden_size_list, output_size=10, activation='relu', weight_init_std='Xavier')- 結果:
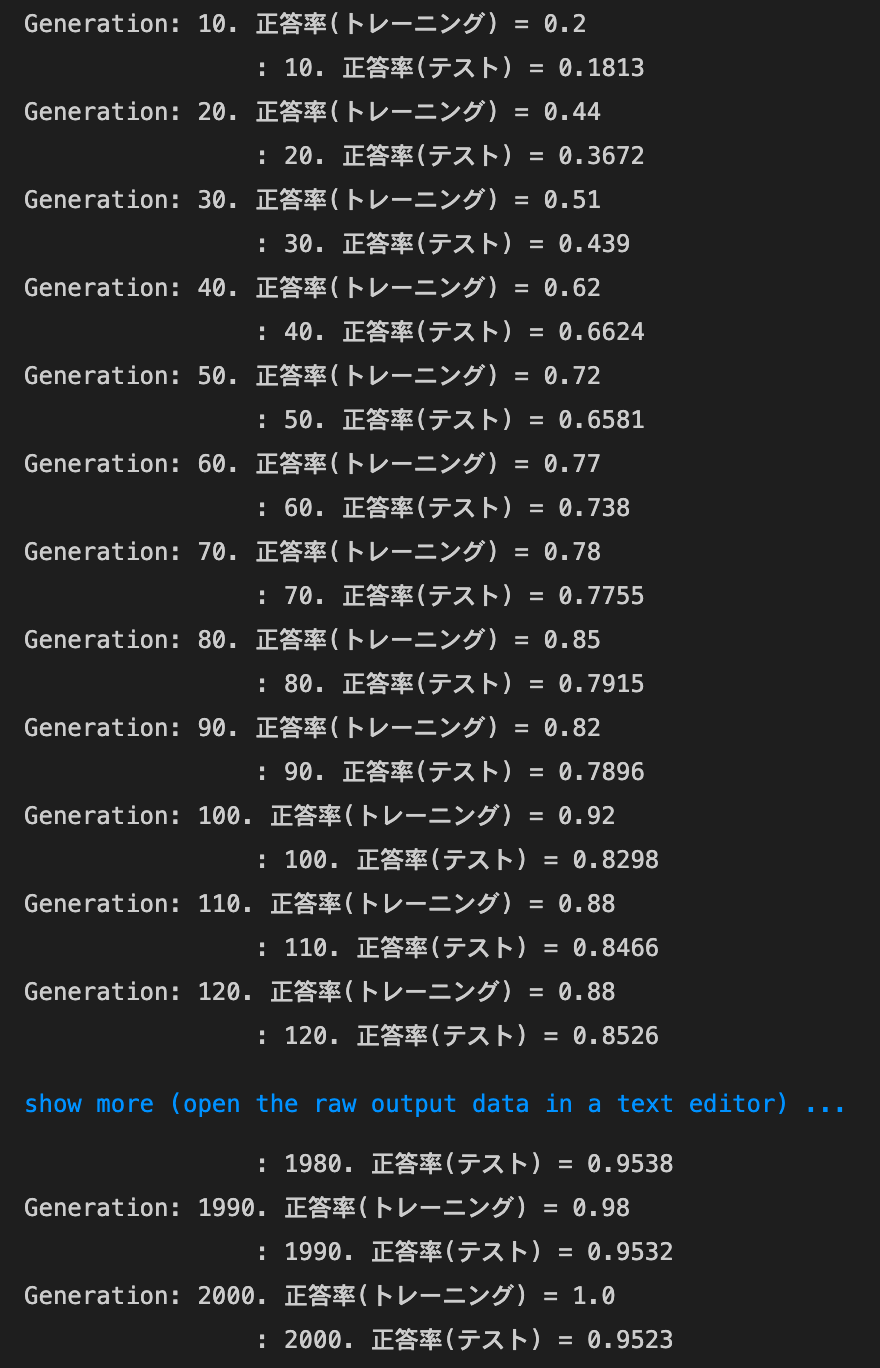
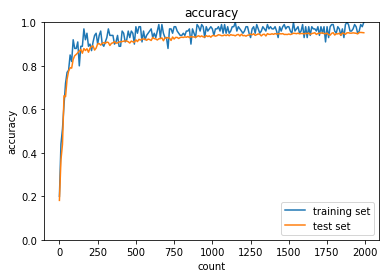
2_3_batch_normalization.ipynb
- デフォルトの実行結果:
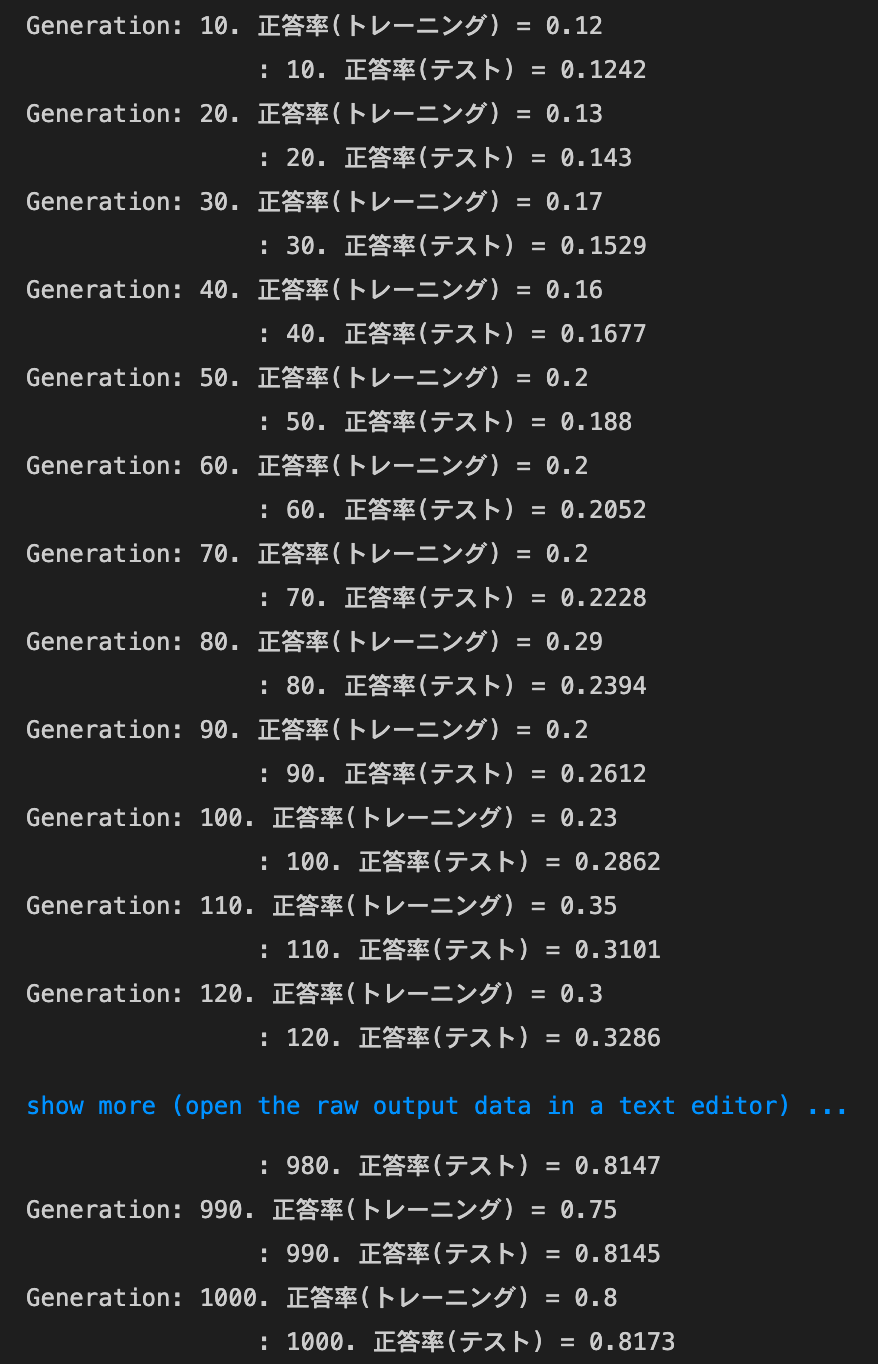
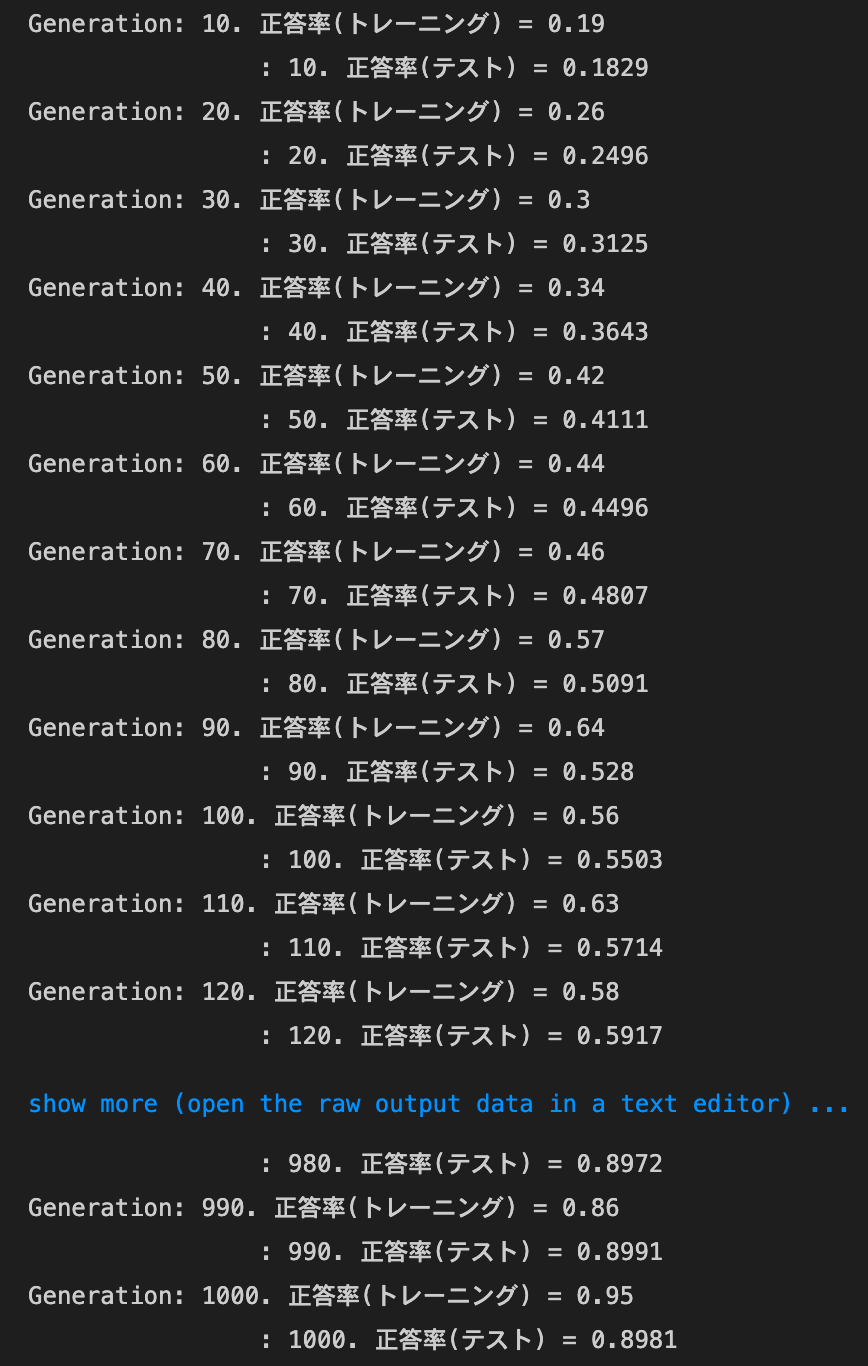
- [try]活性化関数や重みの初期値を変えてみる
networkの初期化処理を、以下のようにしたnetwork = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='he', use_batchnorm=use_batchnorm)- 結果:正答率は上昇した
- トレーニング:0.8 → 0.95
- テスト:0.8173 → 0.8981
2_4_optimizer.ipynb
- デフォルトの実行結果:
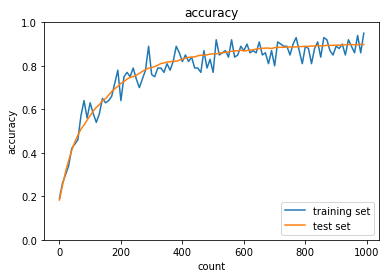
- SGD
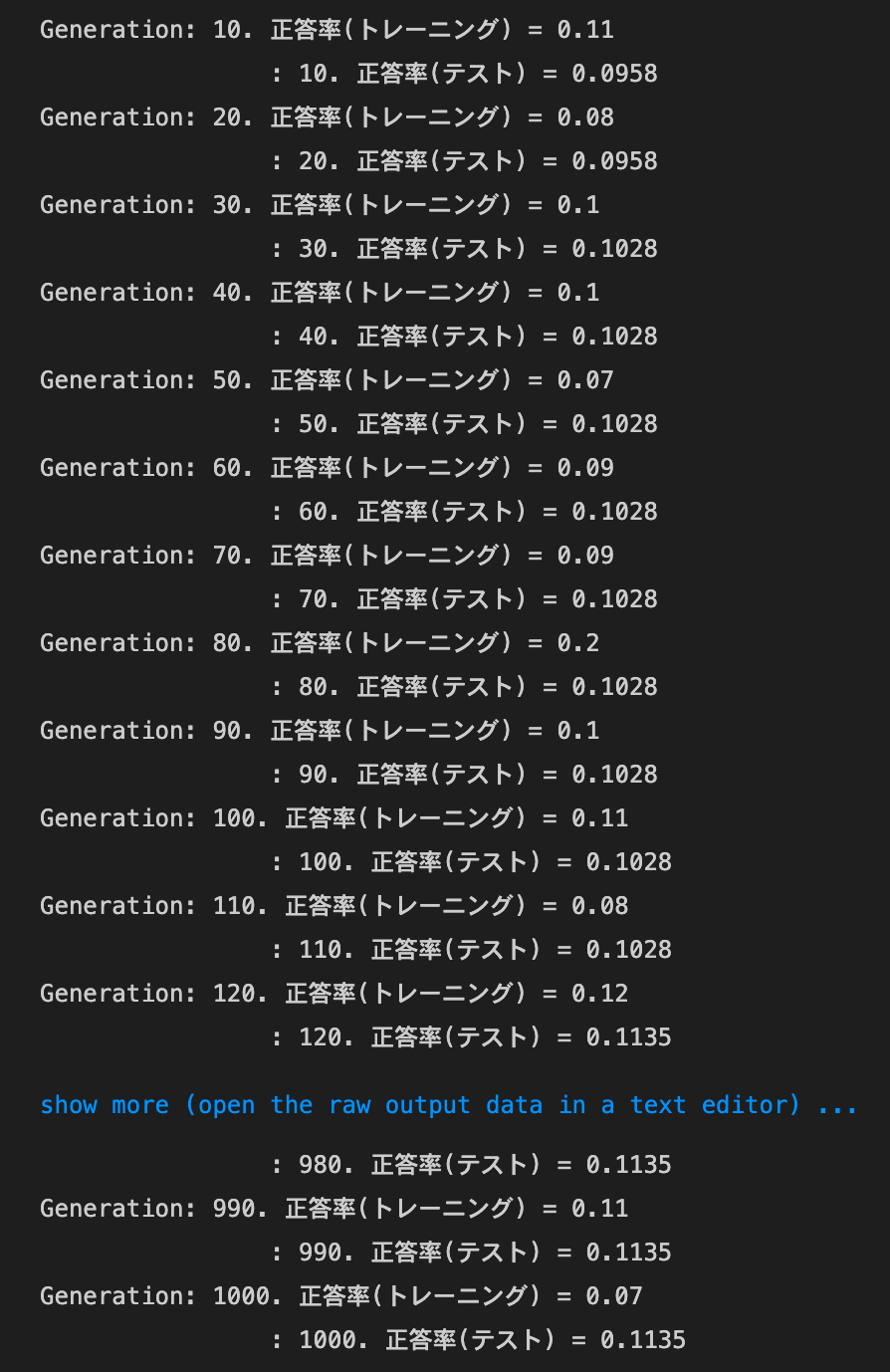
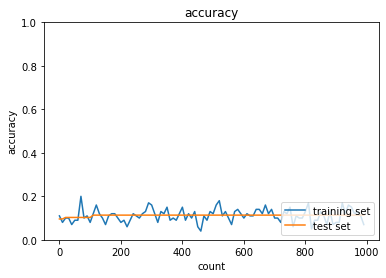
- Momentum
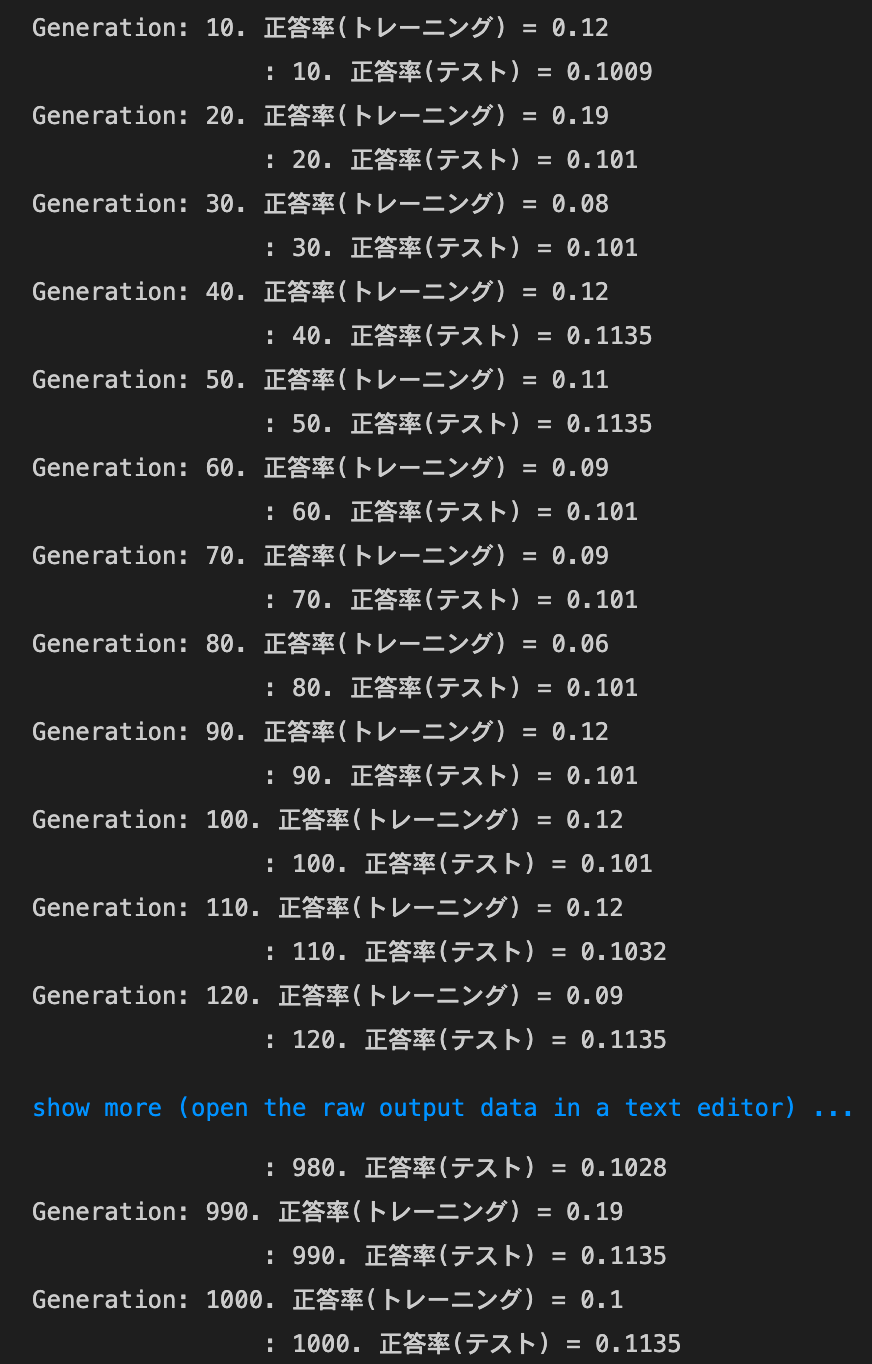
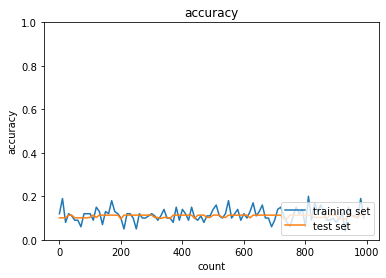
- MomentumをもとにAdaGradを作ってみよう
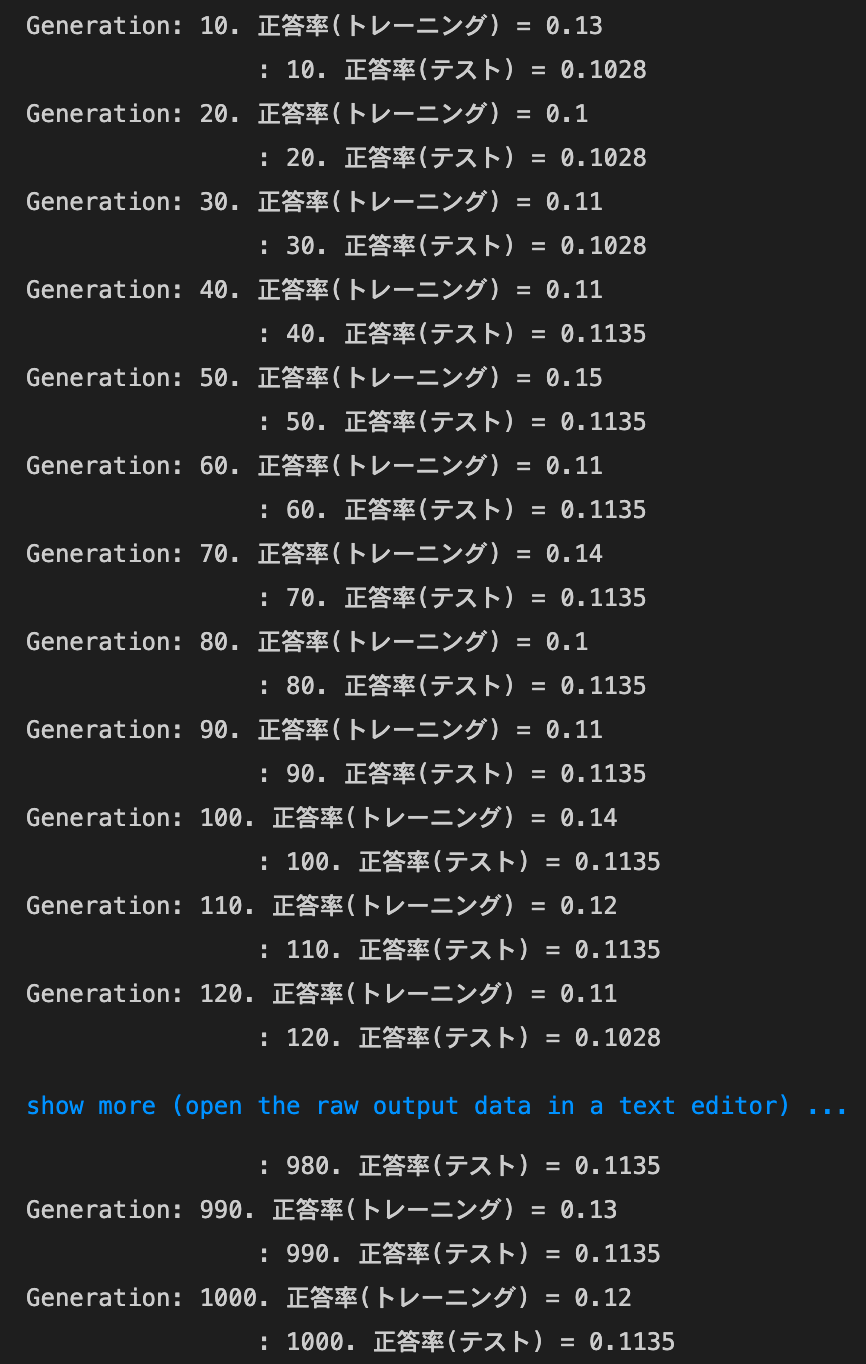
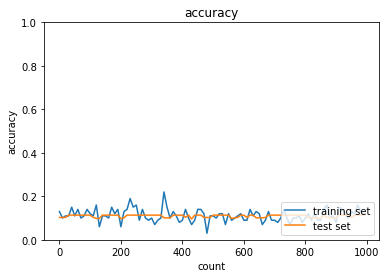
- RMSprop
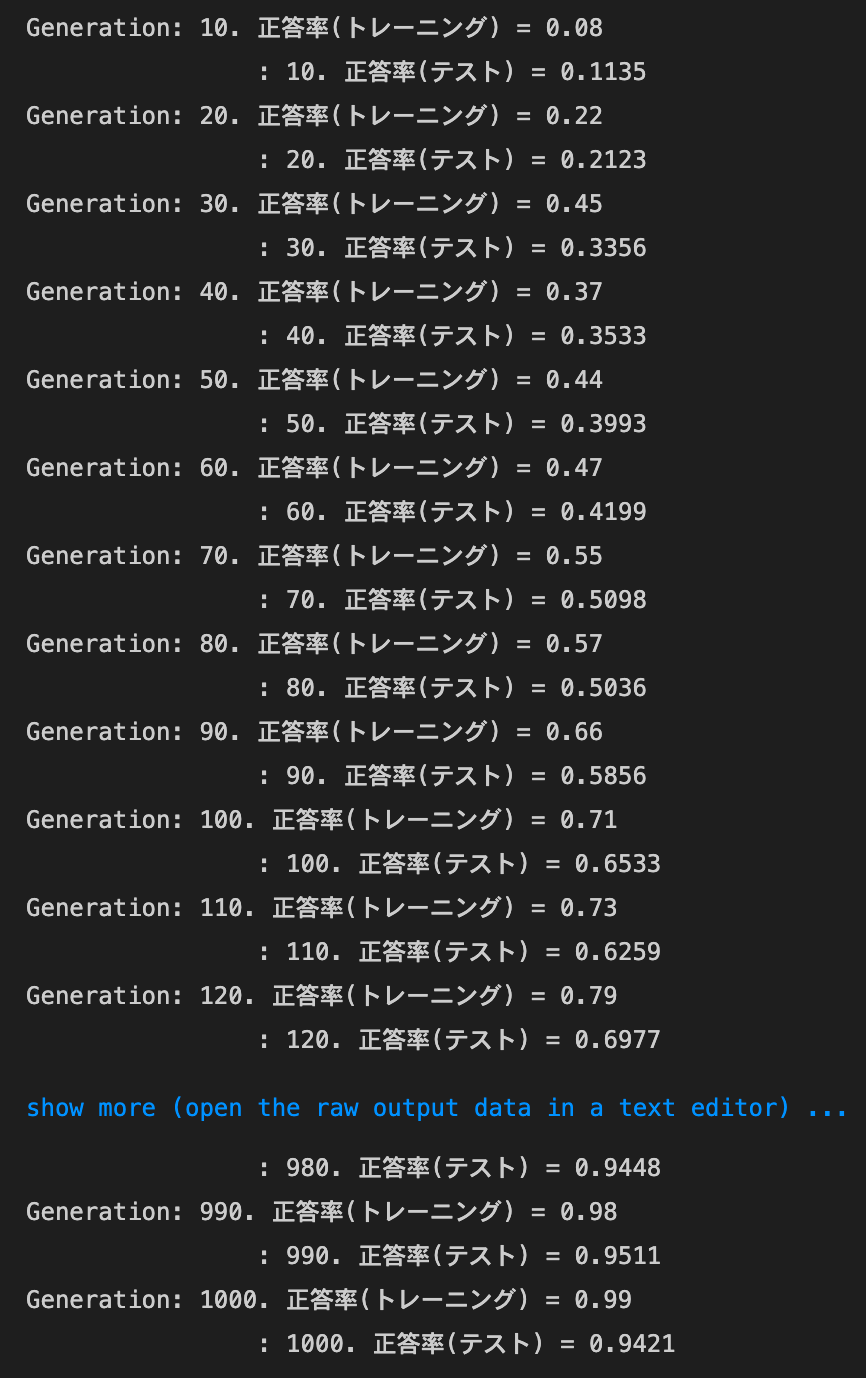
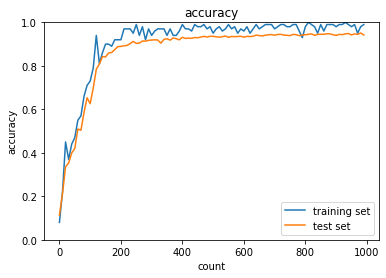
- Adam
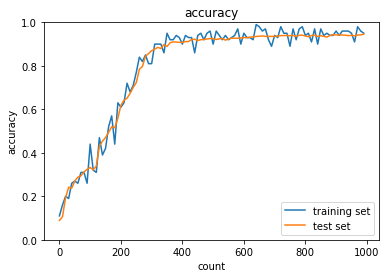
- SGD
- [try]学習率を変えてみる
- 0.01 → 0.1にしてみた結果:
MomentumとAdaGradは正答率向上、RMSpropとAdamは正答率低下。SGDは変化なし- SGD
- トレーニング: 0.07 → 0.17
- テスト: 0.1135 → 0.1135

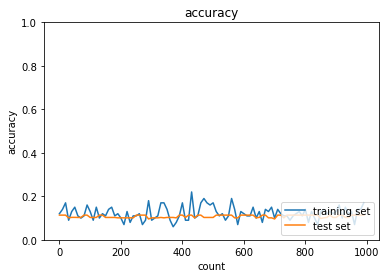
- Momentum
- トレーニング: 0.1 → 0.6
- テスト: 0.1135 → 0.573

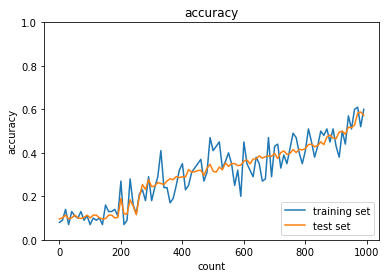
- MomentumをもとにAdaGradを作ってみよう
- トレーニング: 0.12 → 0.76
- テスト: 0.1135 → 0.7306


- RMSprop
- トレーニング: 0.99 → 0.21
- テスト: 0.9421 → 0.1028

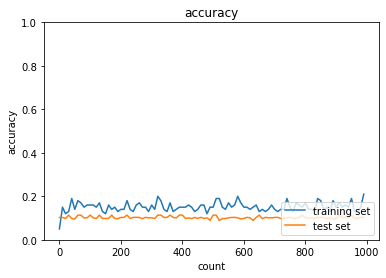
- Adam
- トレーニング: 0.95 → 0.09
- テスト: 0.9456 → 0.1028

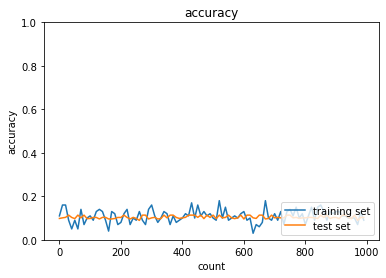
- SGD
- 0.01 → 0.1にしてみた結果:
- [try]活性化関数と重みの初期か方法を変えてみる
- 活性化関数はReLU, 初期化方法はXavierにしてみる
- コード
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='xavier', use_batchnorm=use_batchnorm) - 結果:SGD, Momentum, AdaGradで正答率が大きく向上、他はあまり変化なし
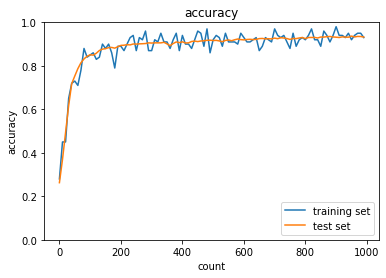
- SGD
- トレーニング: 0.07 → 0.87
- テスト: 0.1135 → 0.8801

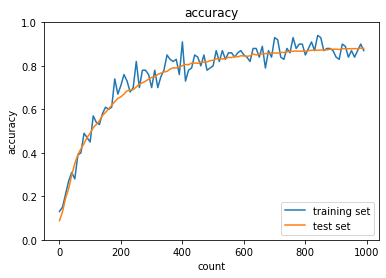
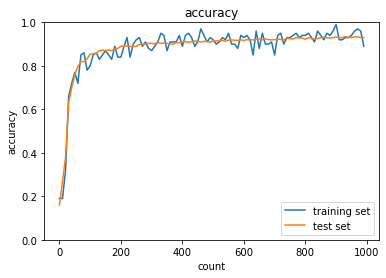
- Momentum
- トレーニング: 0.1 → 0.93
- テスト: 0.1135 → 0.9325

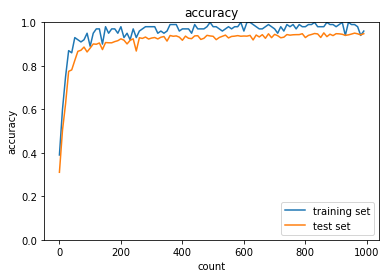
- MomentumをもとにAdaGradを作ってみよう
- トレーニング: 0.12 → 0.89
- テスト: 0.1135 → 0.9296

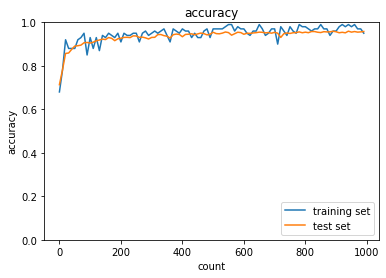
- RMSprop
- トレーニング: 0.99 → 0.96
- テスト: 0.9421 → 0.9479

- Adam
- トレーニング: 0.95 → 0.95
- テスト: 0.9456 → 0.958

- SGD
- コード
- 活性化関数はReLU, 初期化方法はXavierにしてみる
- [try]バッチ正規化をしてみる
- 結果:
SGD, Momentum, AdaGradは正答率が大きく向上、RMSpropとAdamはわずかに低下
ただ、RMSpropとAdamでも比較的少ない試行回数で正答率が向上するようになった- SGD
- トレーニング: 0.07 → 0.71
- テスト: 0.1135 → 0.6722

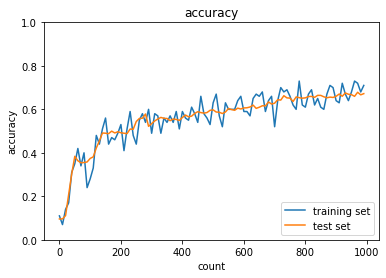
- Momentum
- トレーニング: 0.1 → 0.87
- テスト: 0.1135 → 0.8984

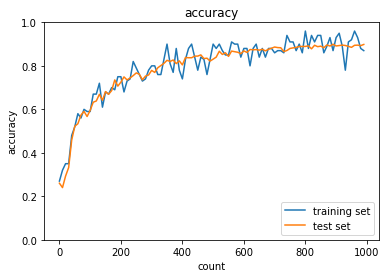
- MomentumをもとにAdaGradを作ってみよう
- トレーニング: 0.12 → 0.93
- テスト: 0.1135 → 0.8882

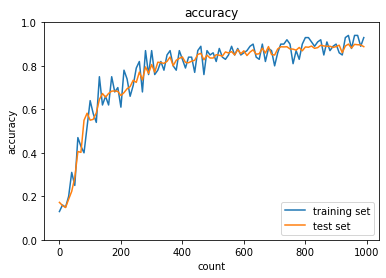
- RMSprop
- トレーニング: 0.99 → 0.98
- テスト: 0.9421 → 0.9265

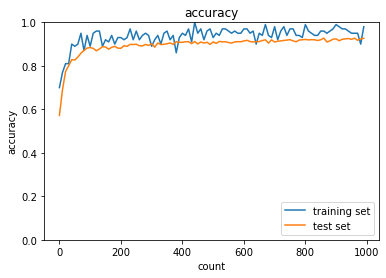
- Adam
- トレーニング: 0.95 → 0.95
- テスト: 0.9456 → 0.9228

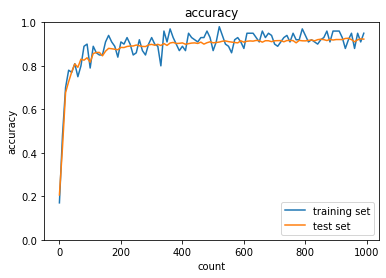
- SGD
- 結果:
2_5_overfitting.ipynb
overfitting
実行結果
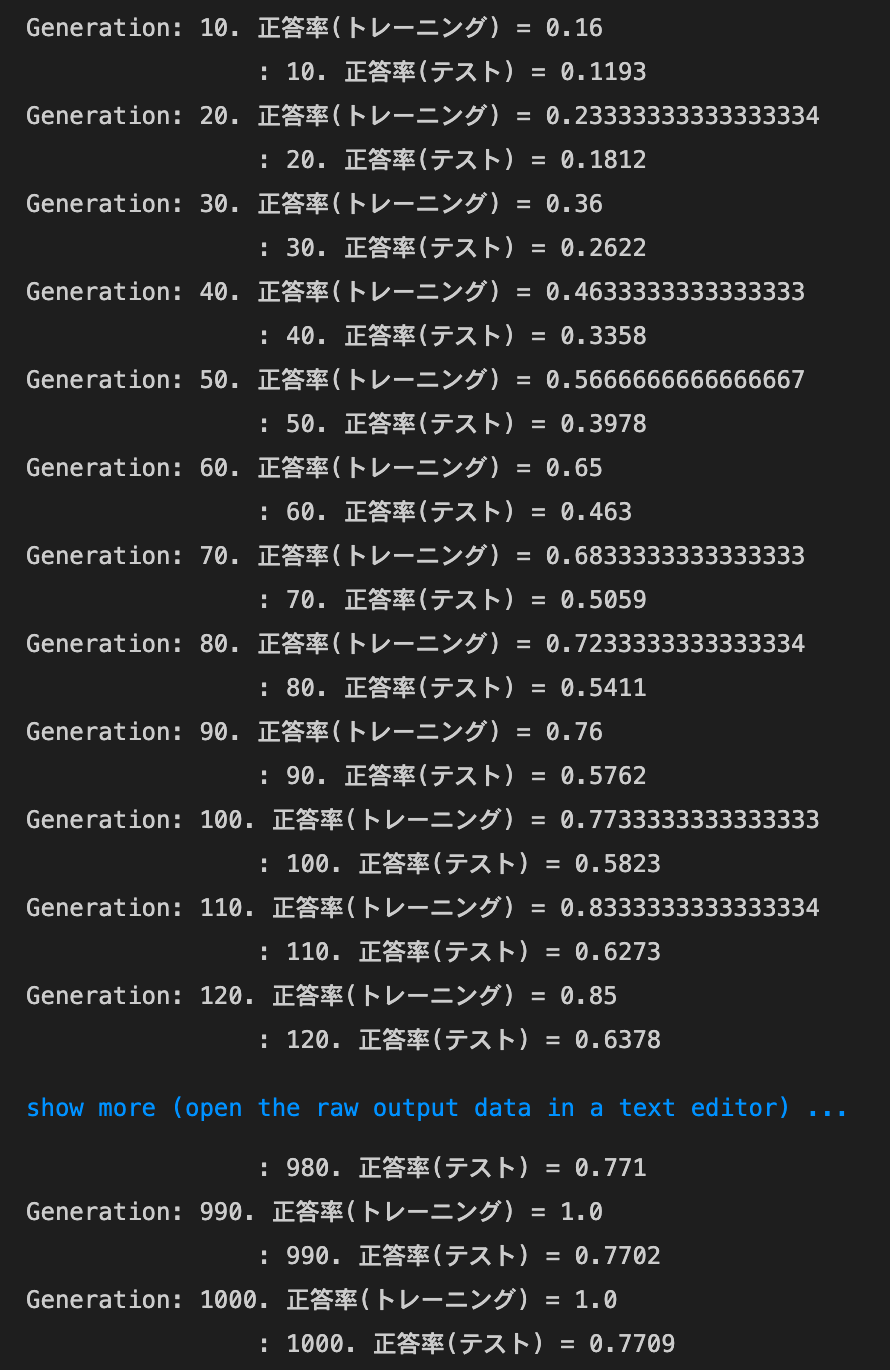
weight decay - L2
- 実行結果
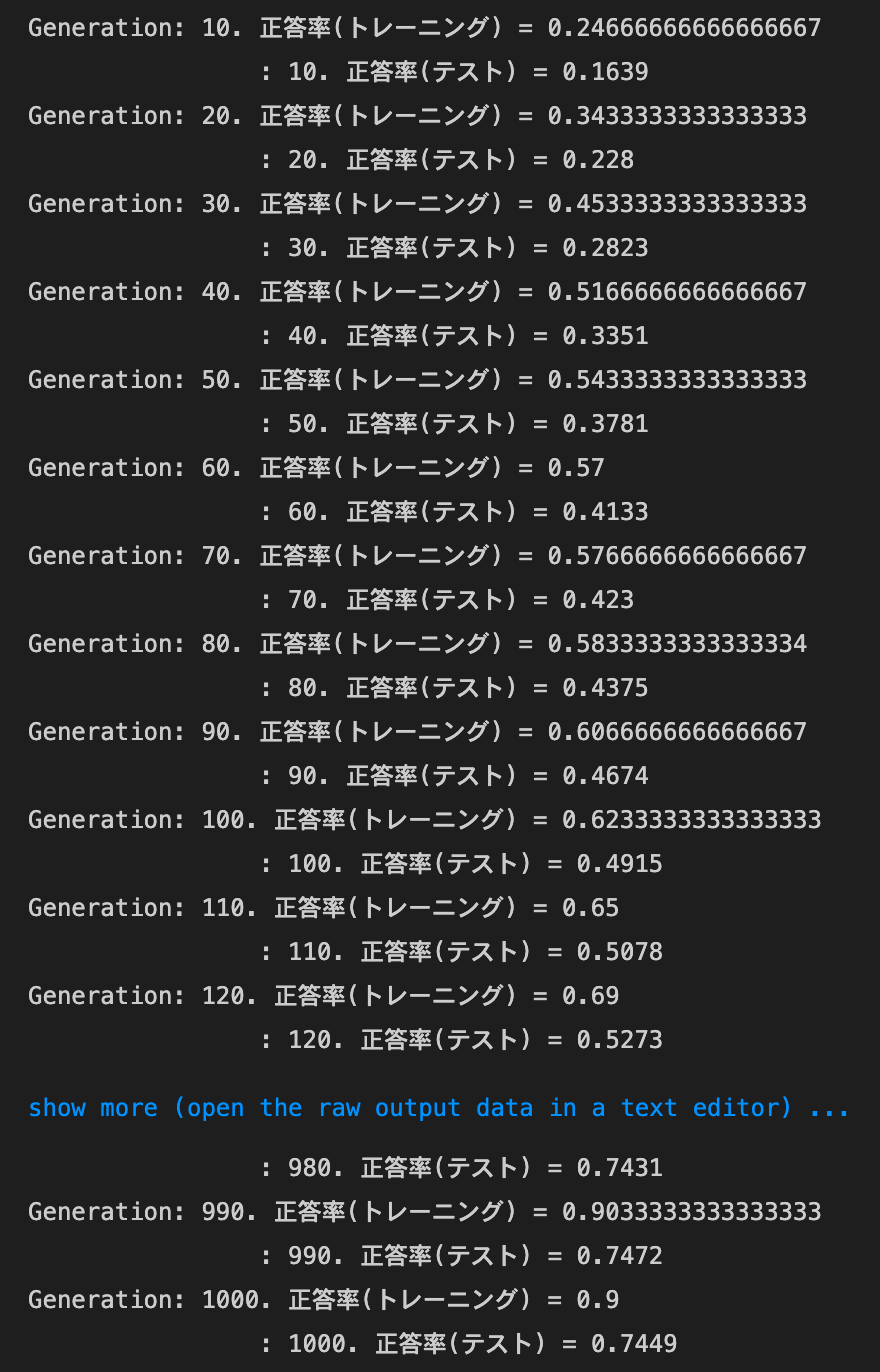
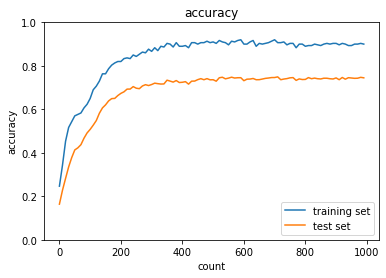
- [try]
weight_decay_lambdaの値を変更して正則化の強さを確認するweight_decay_lambdaが0.01の場合
→効果が全くない
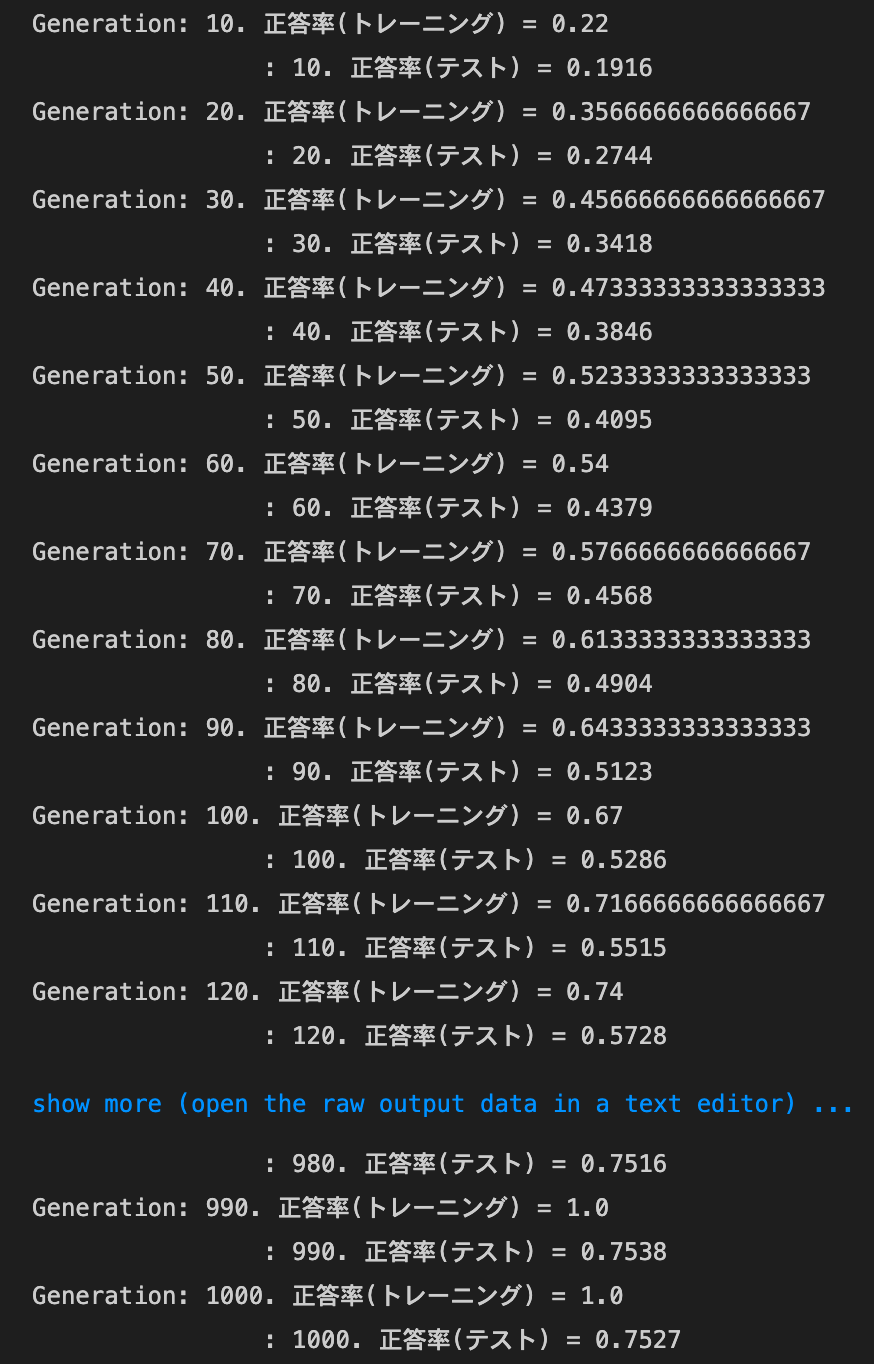
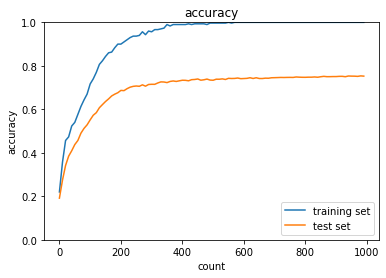
weight_decay_lambdaが0.15の場合
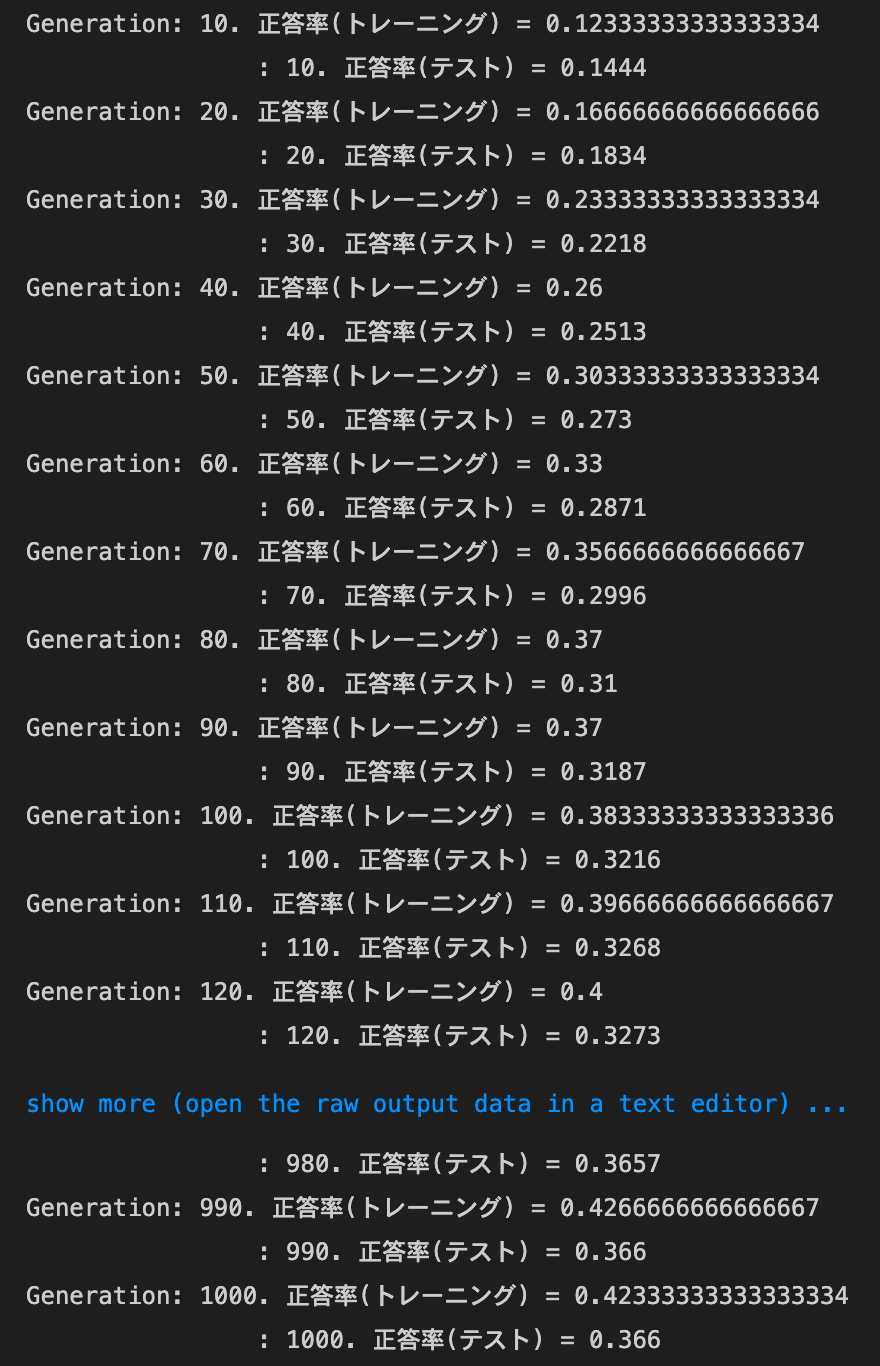
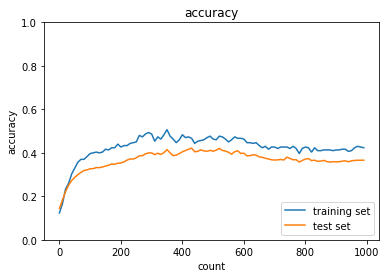
weight_decay_lambdaが0.5の場合
→途中から精度が落ち、そのまま横ばいになってしまった
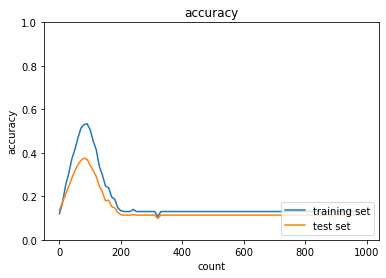
weight decay - L1
- 実行結果
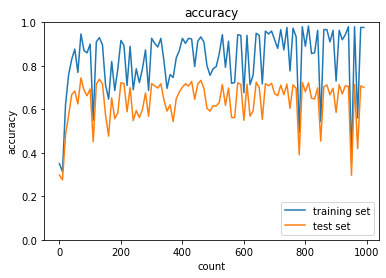
- [try]
weight_decay_lambdaの値を変更して正則化の強さを確認するweight_decay_lambdaが0.005の場合
→正答率は早く上がったが、過学習になってしまった
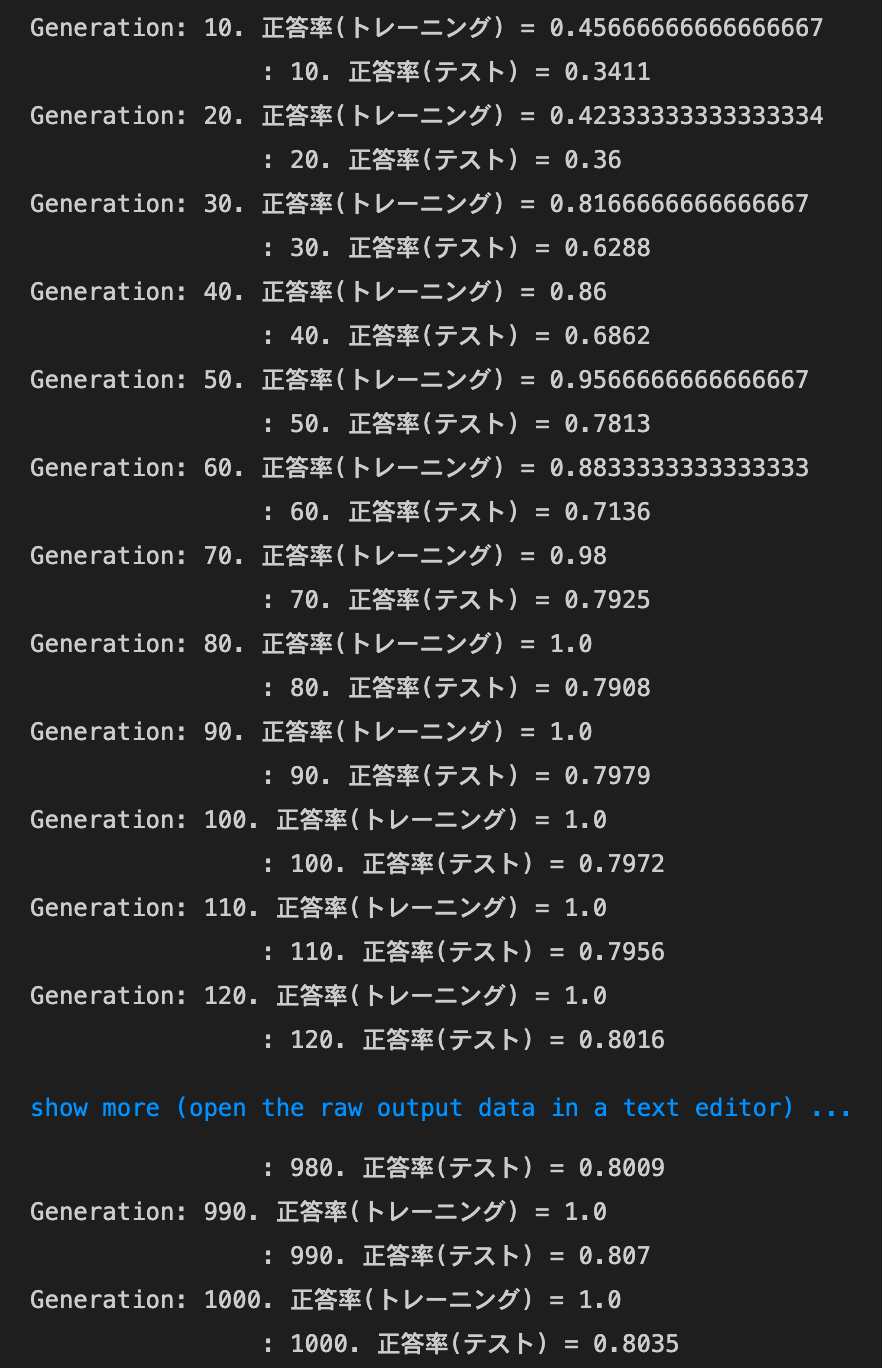
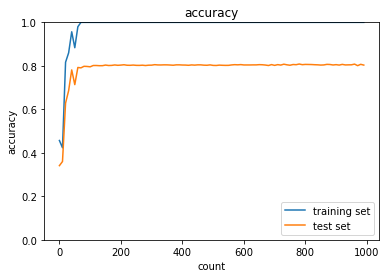
weight_decay_lambdaが0.1の場合
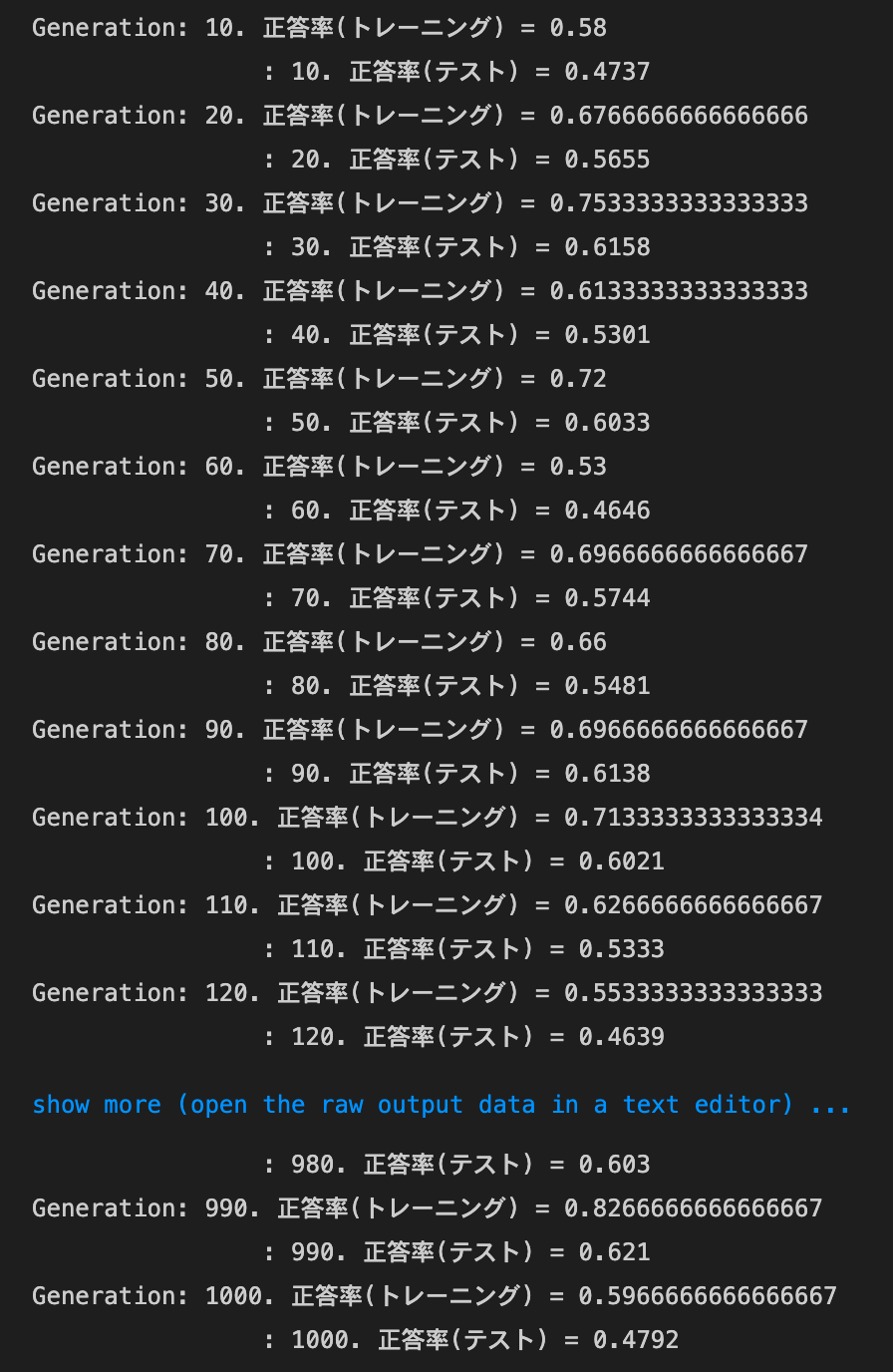
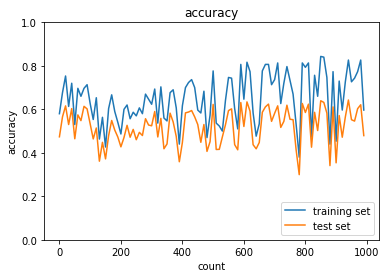
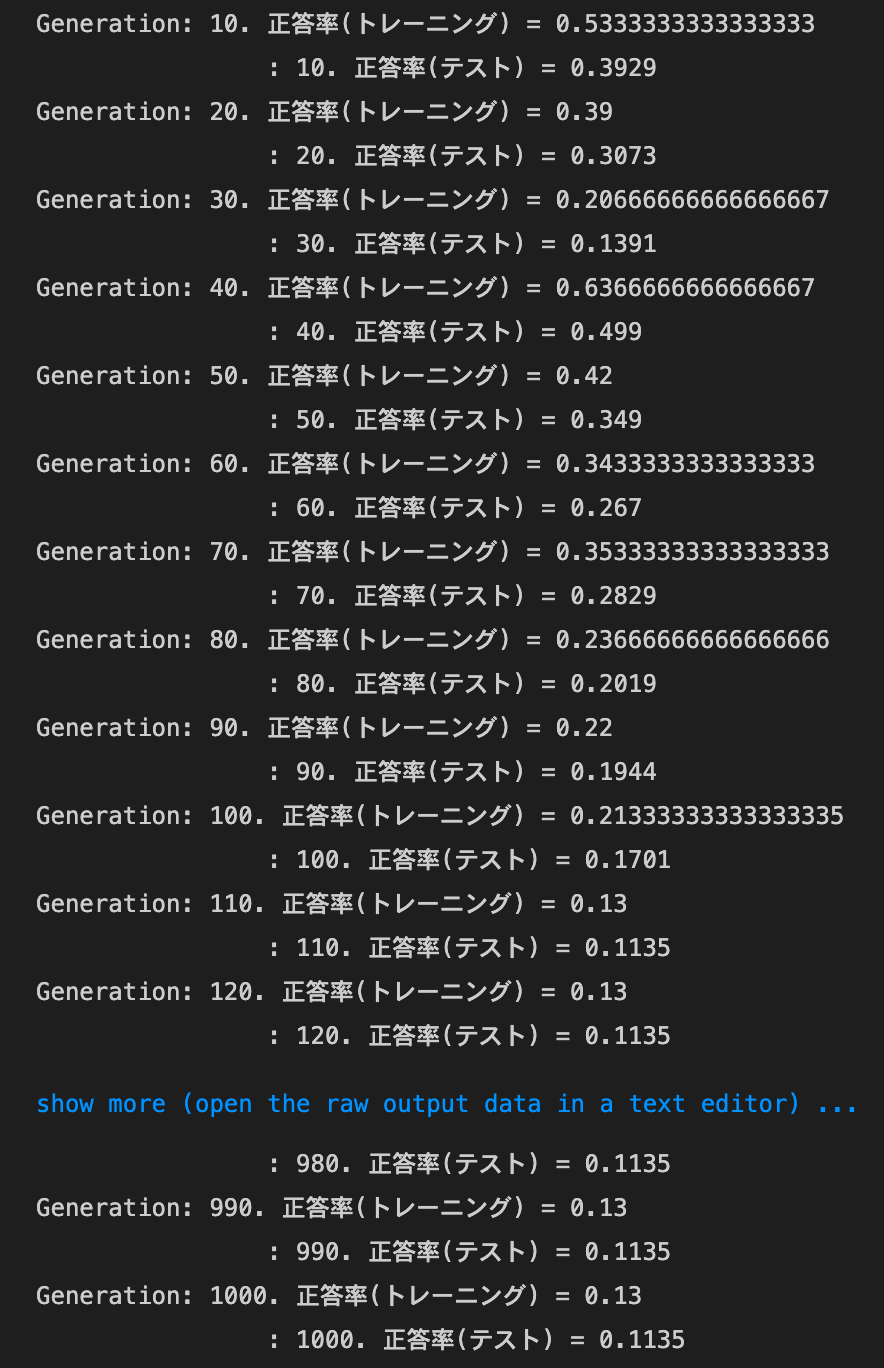
weight_decay_lambdaが0.15の場合
→途中から精度が落ち、そのまま横ばいになってしまった
Dropout
- 実行結果
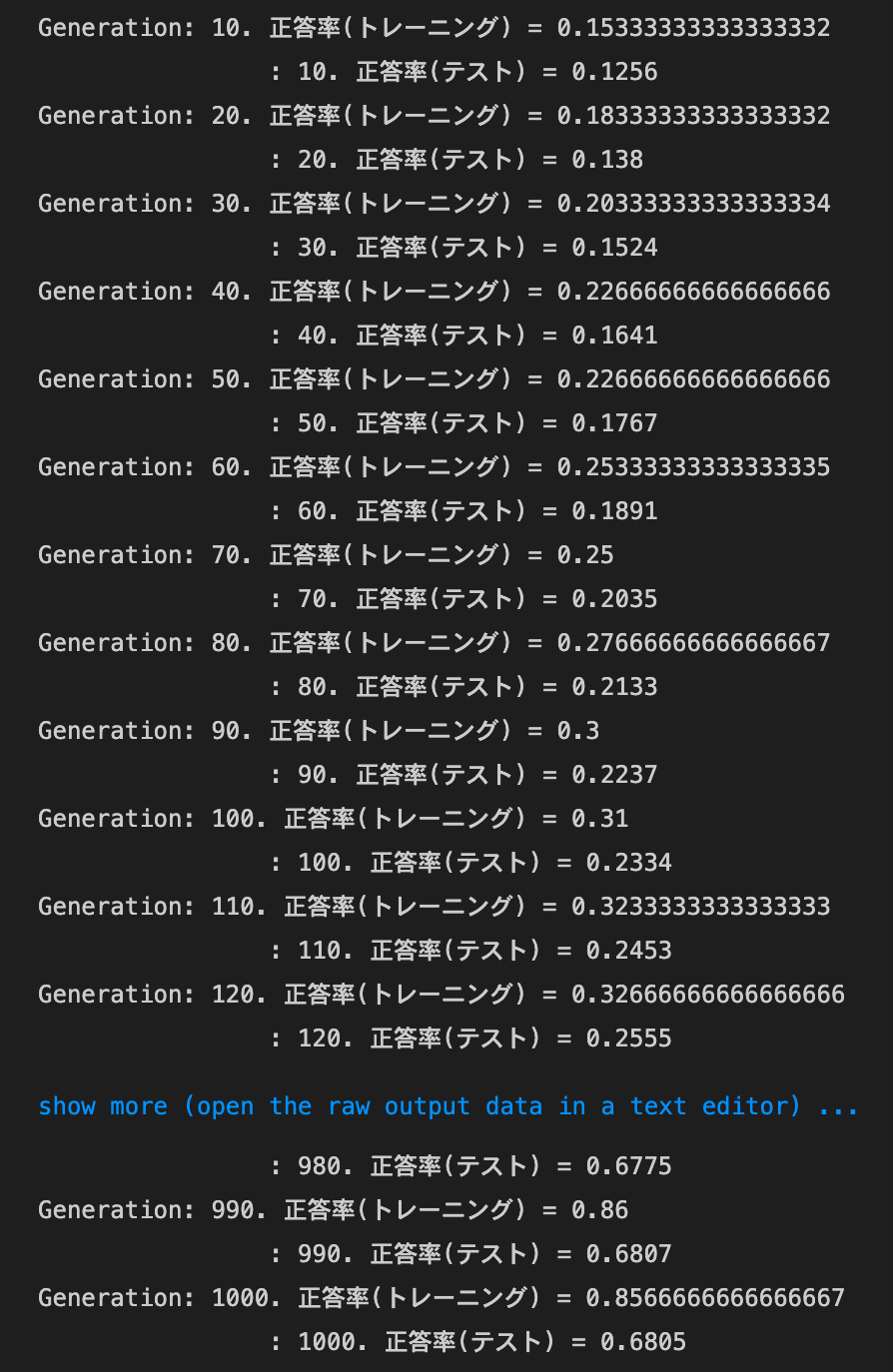
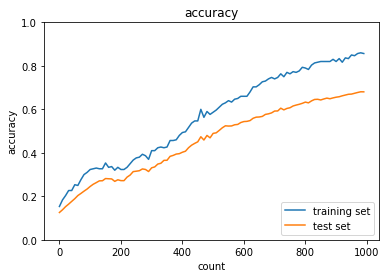
- [try]
dropout_ratioの値を変更してみるdropout_ratioが0.1の場合
→正答率は上がったものの、過学習している
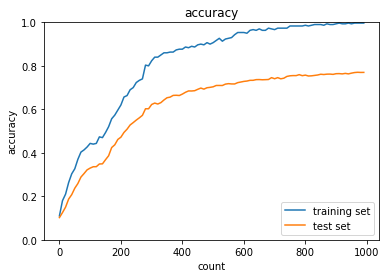
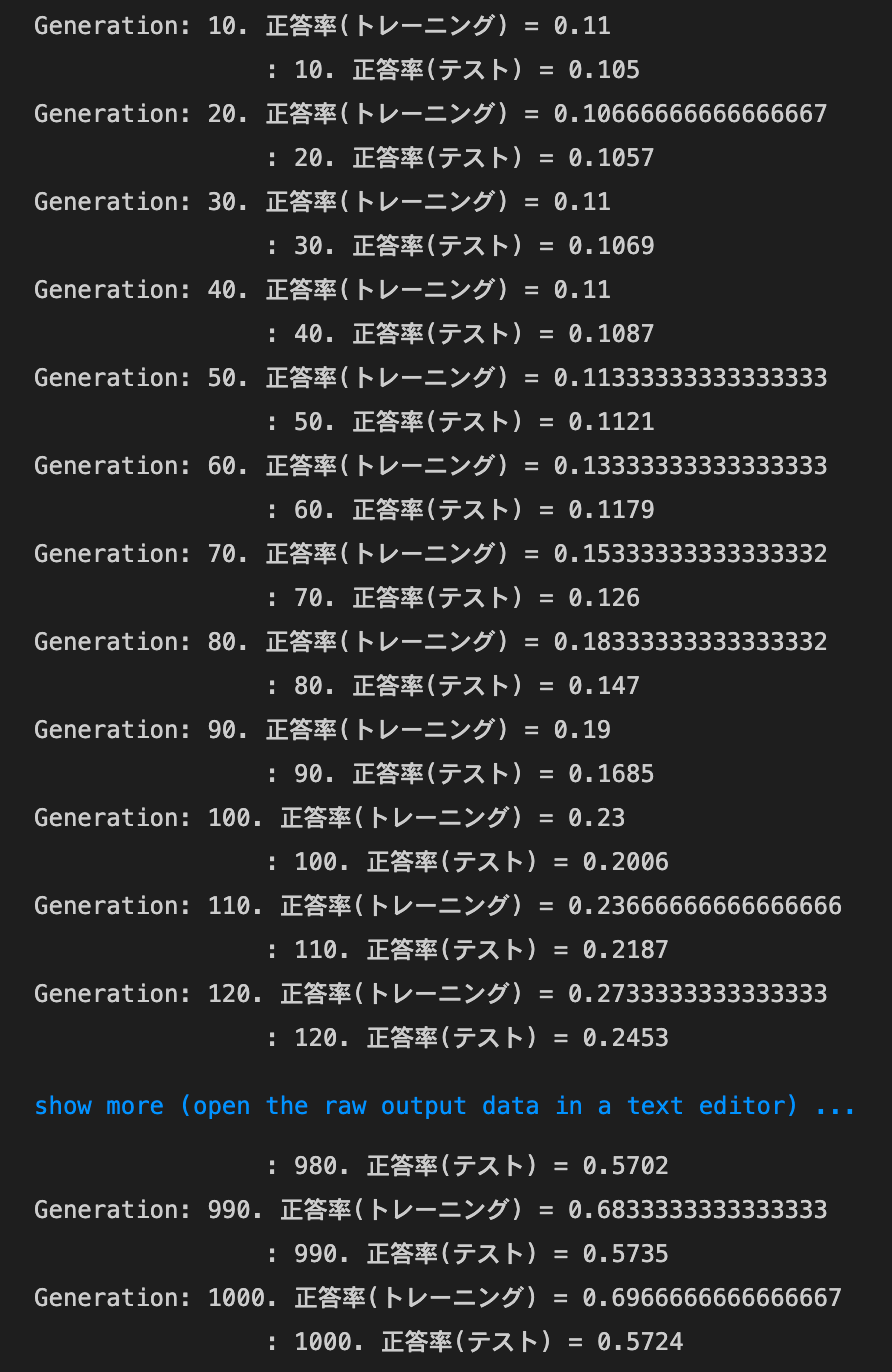
dropout_ratioが0.2の場合
→正答率は十分には上がらなかったが、トレーニングデータとテストデータの正答率の差は縮まった
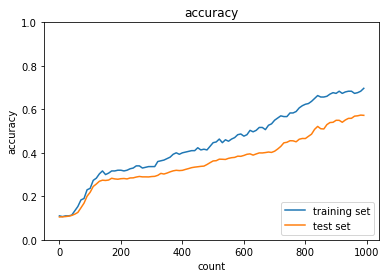
- [try]
optimizerとdropout_ratioの値を変更してみるoptimizer:Momentum,dropout_ratio:0.1の場合
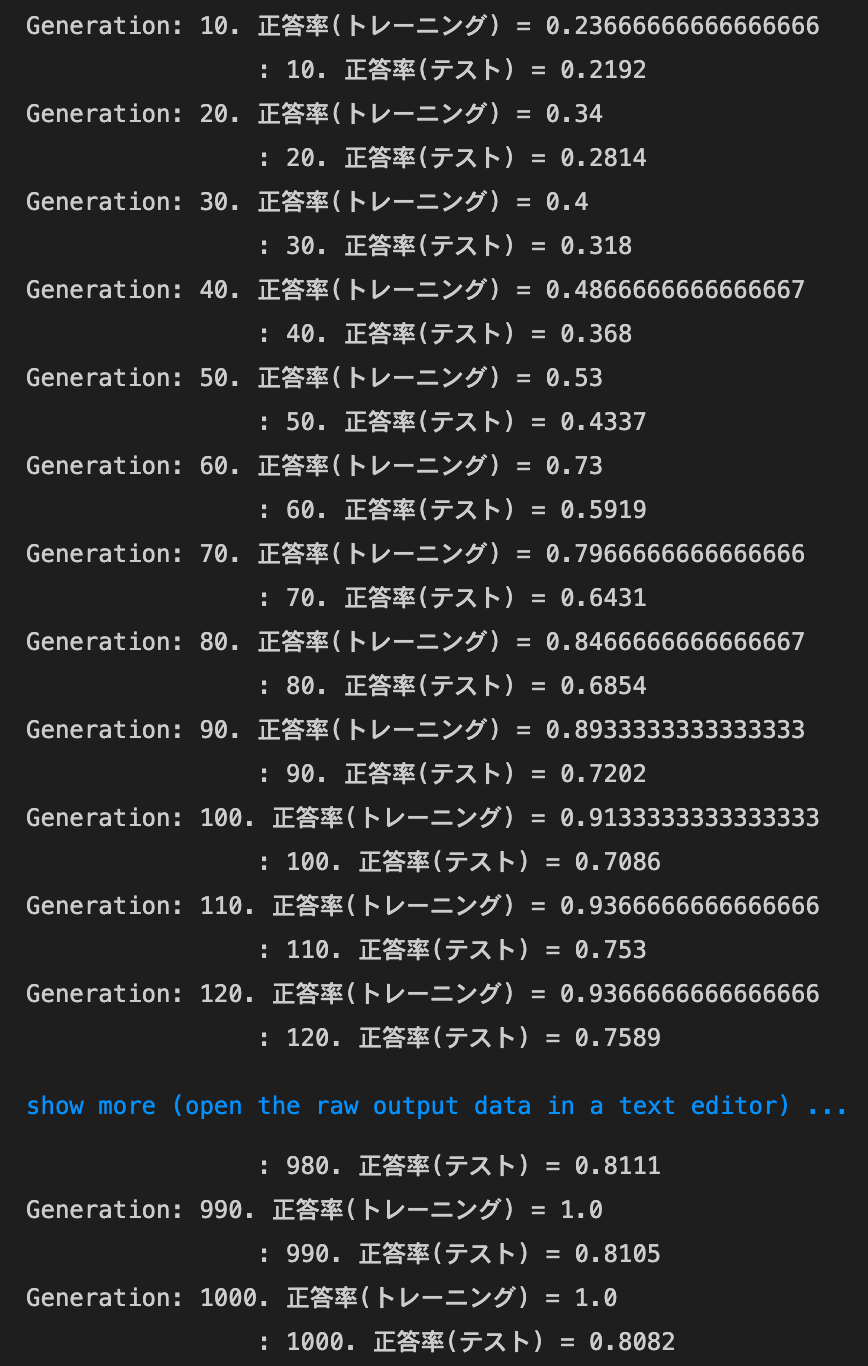
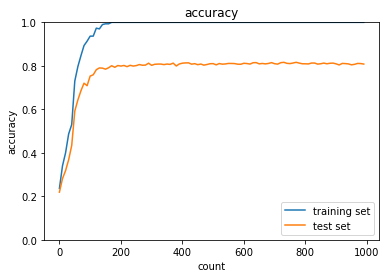
optimizer:AdaGrad,dropout_ratio:0.1の場合
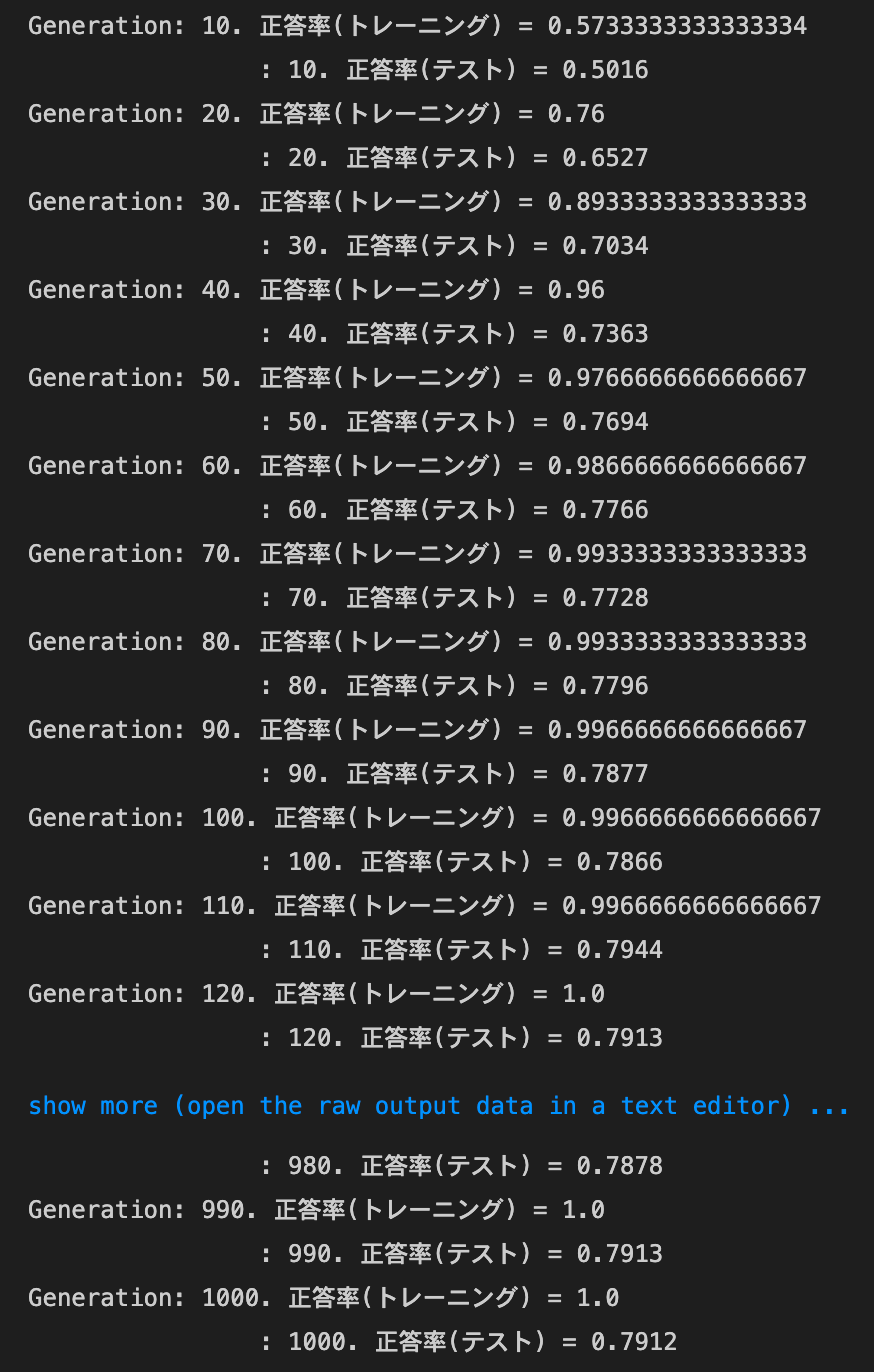
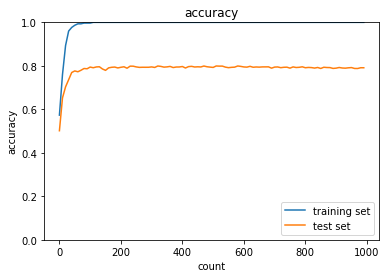
optimizer:Adam,dropout_ratio:0.1の場合
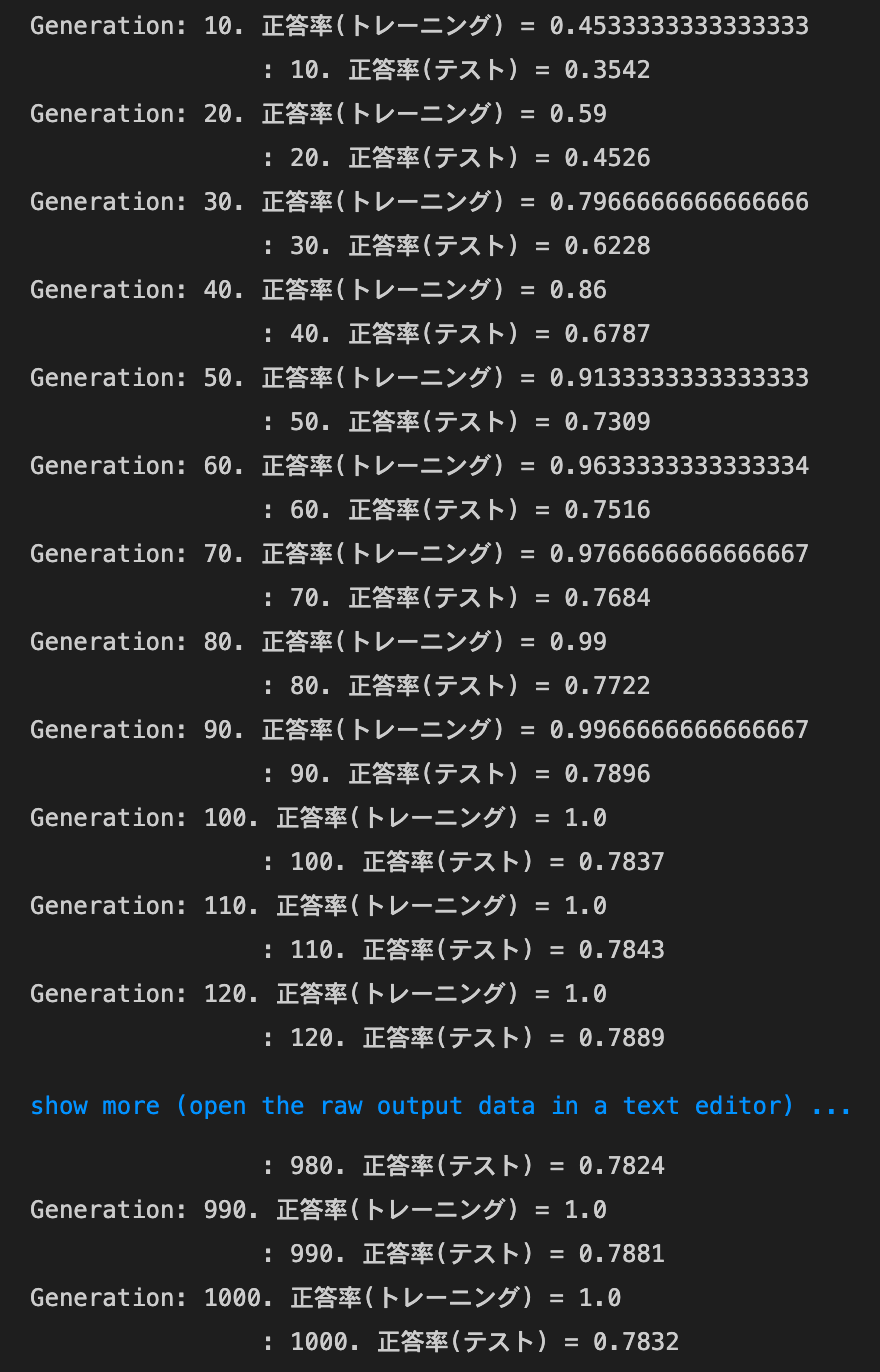
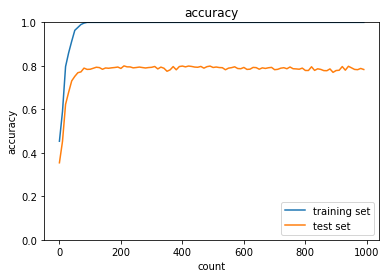
optimizer:Momentum,dropout_ratio:0.35の場合
(SGDの場合と違い、dropout_ratioが0.2でも過学習した。0.35くらいがちょうど良さそう)
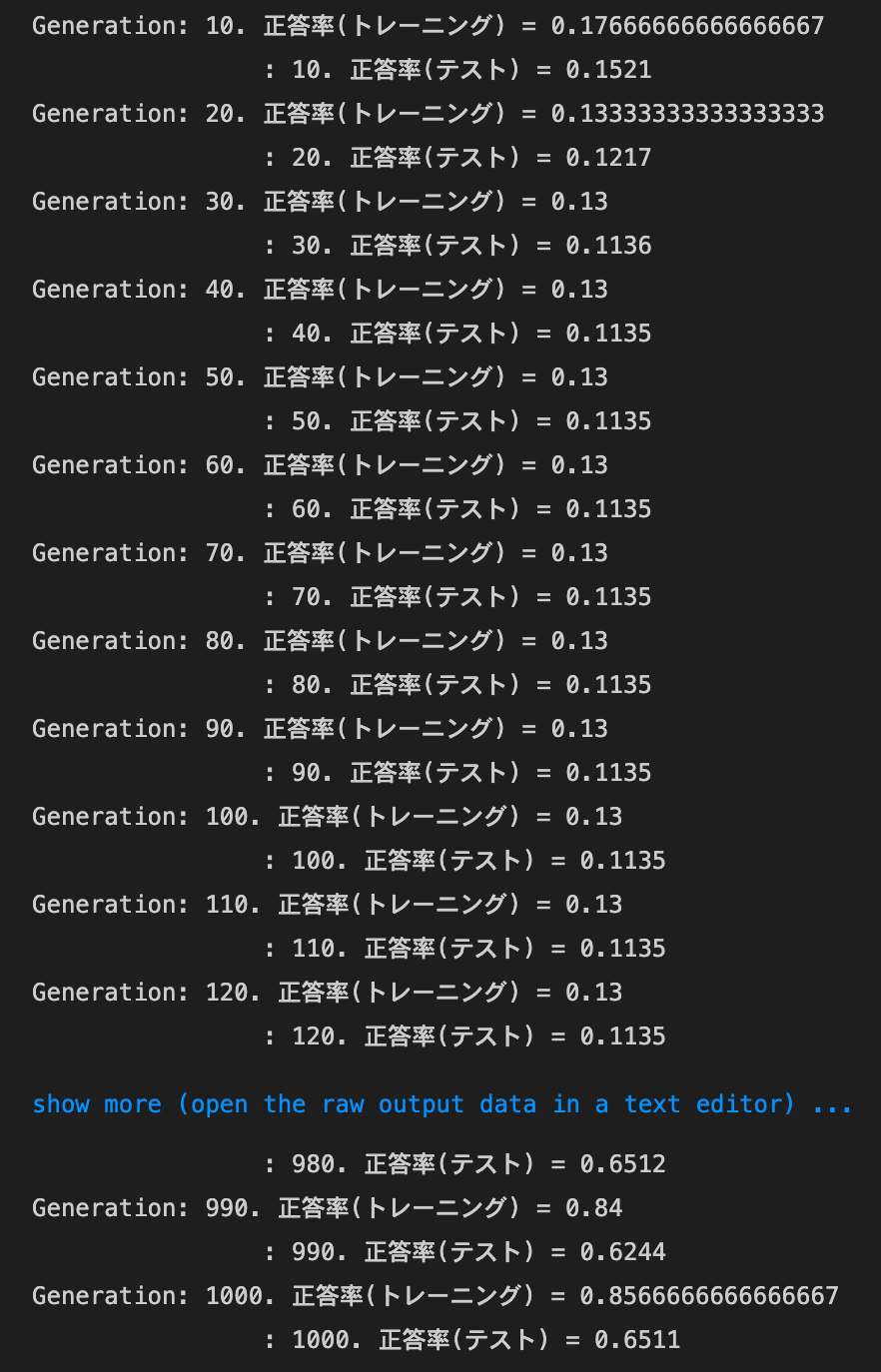
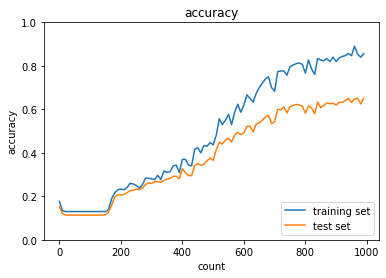
optimizer:AdaGrad,dropout_ratio:0.425の場合
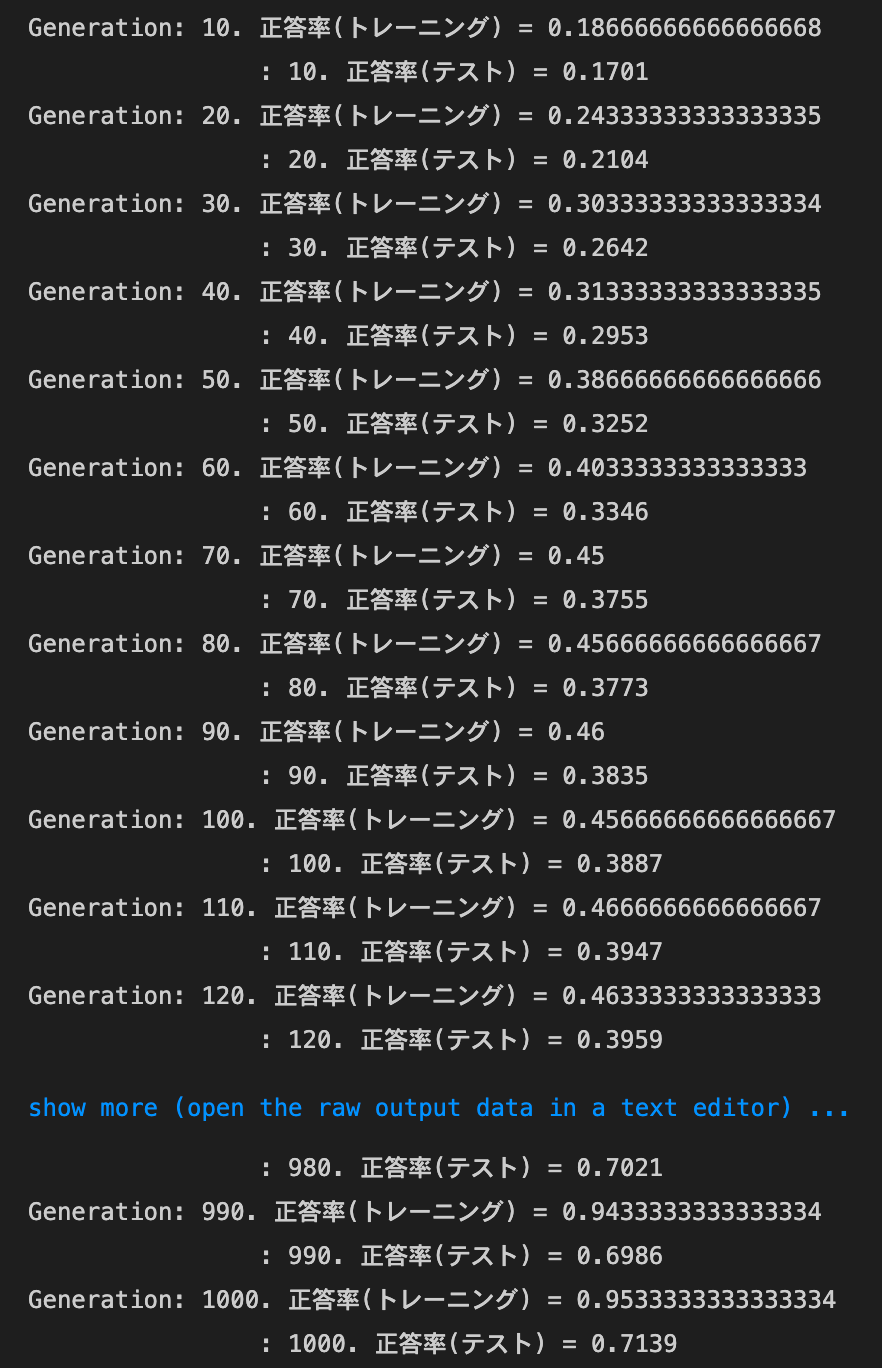
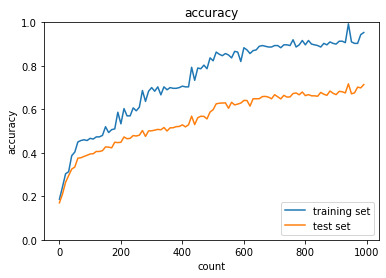
optimizer:Adam,dropout_ratio:0.437の場合
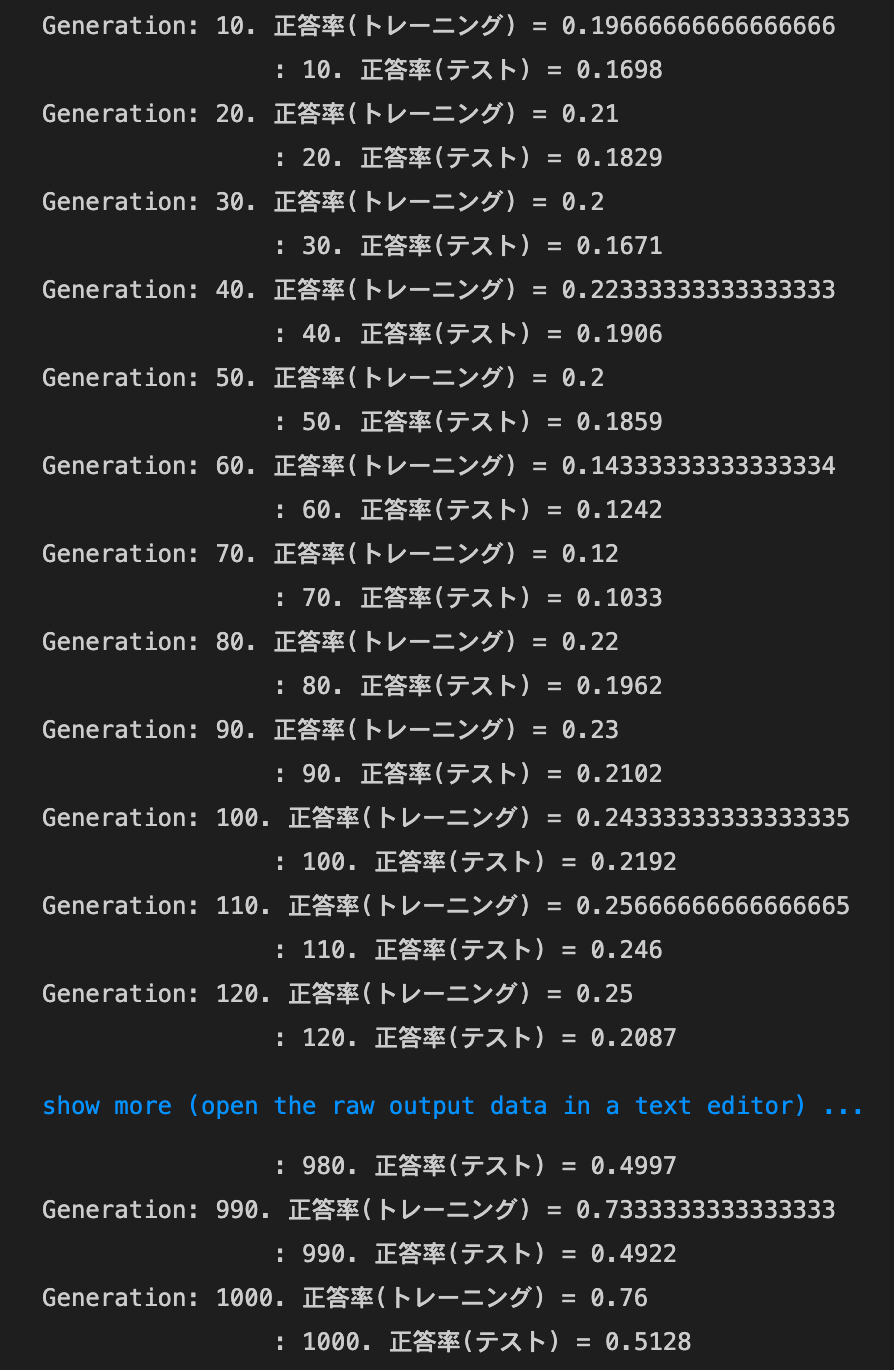
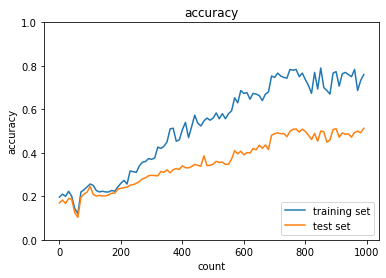
Dropout + L1
実行結果
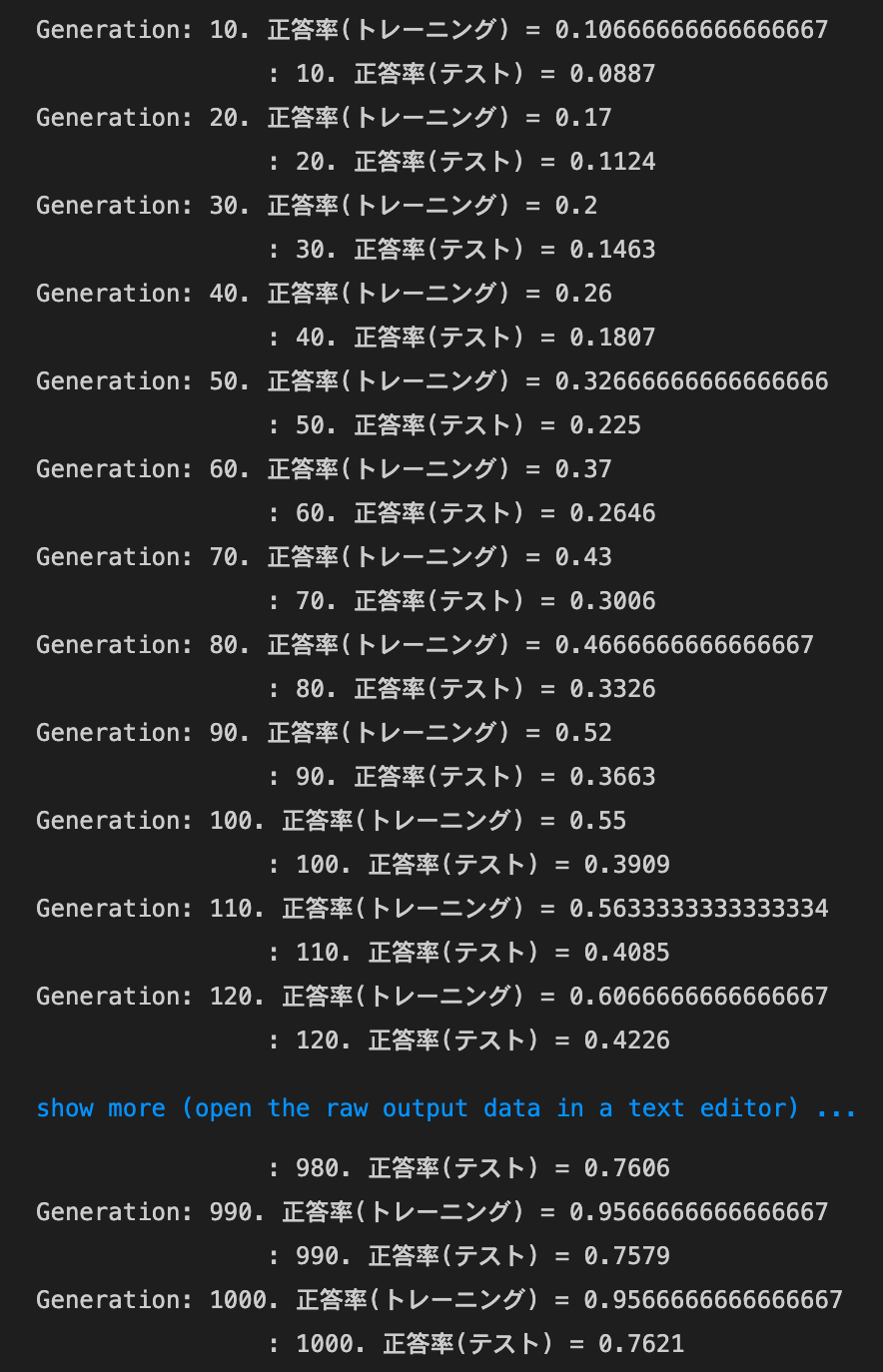
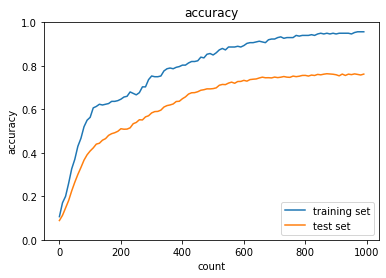
2_6_simple_convolution_network_after.ipynb
image to column
- 実行結果
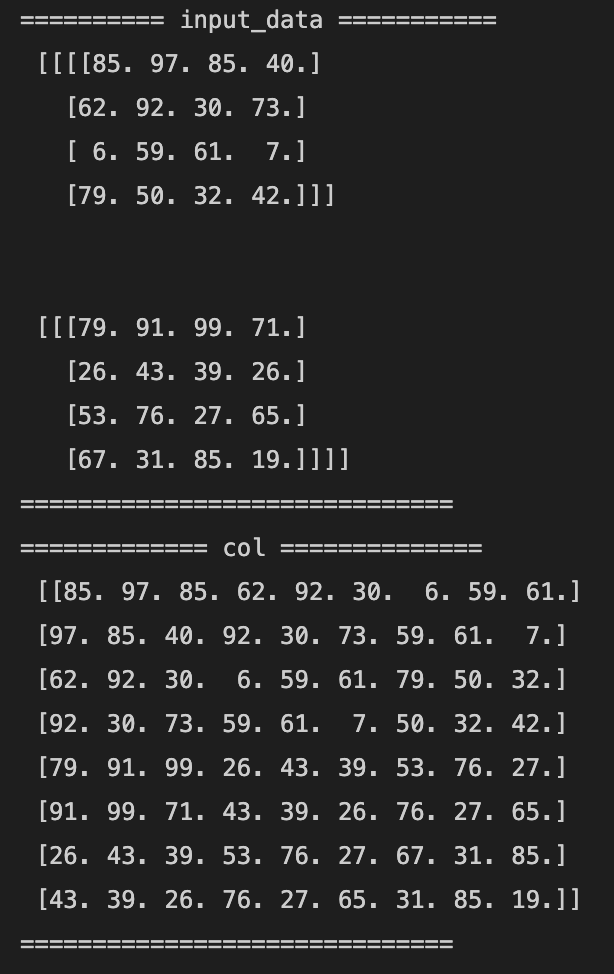
- [try]
im2colの処理を確認する- 関数内で
transposeの処理をしている行をコメントアウトして下のコードを実行してみる
→要素の順番が変わってしまった
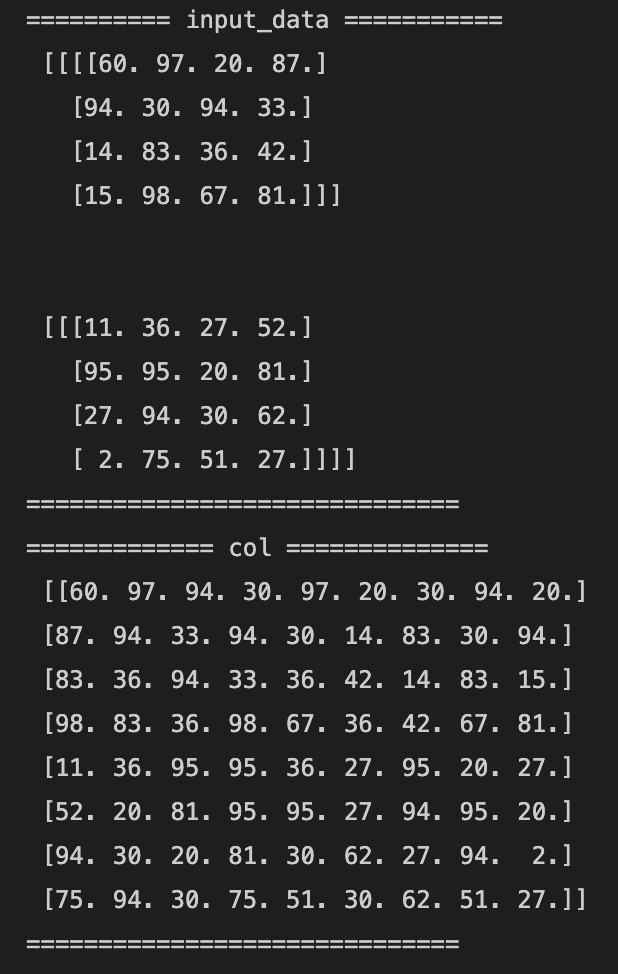
input_dataの各次元のサイズやフィルターサイズ・ストライド・パディングを変えてみる- 以下のように変えた結果
number: 3channel: 2width: 6height: 6filter_w: 4filter_h: 4stride: 2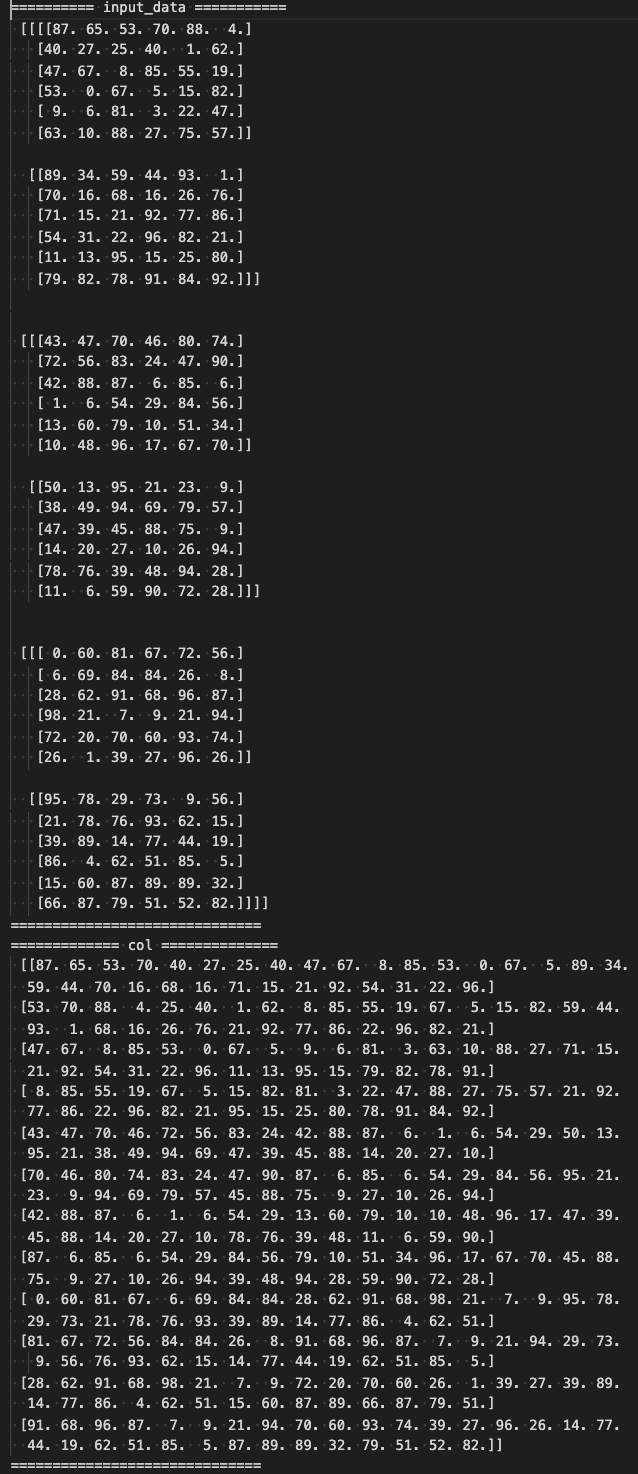
- 以下のように変えた結果
- 関数内で
- [try]
col2imの処理を確認するim2colの確認で出力したcolをimageに変換して確認する
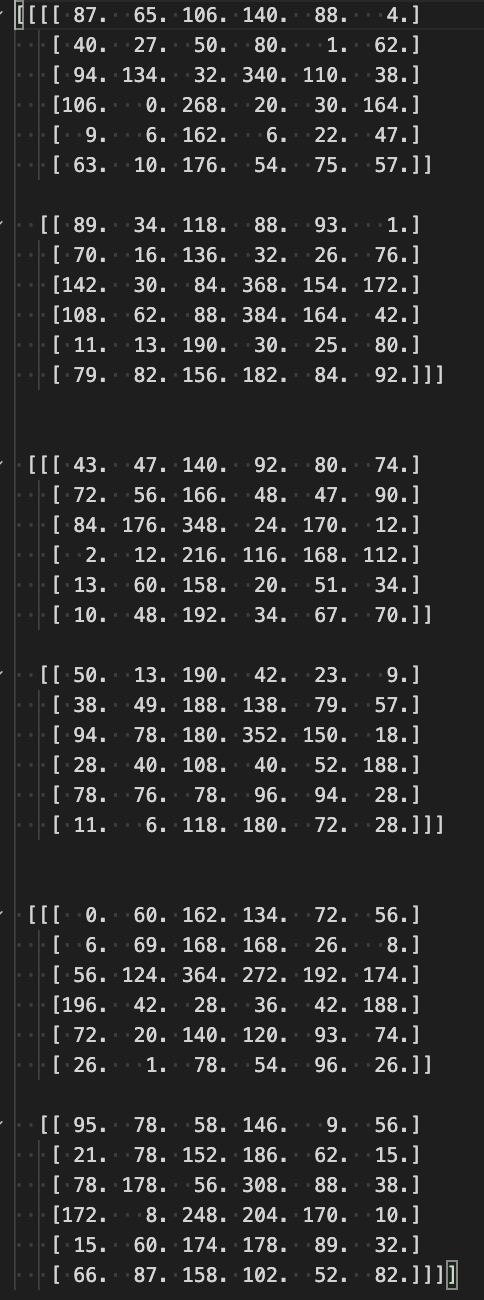
simple convolution network class
実行結果
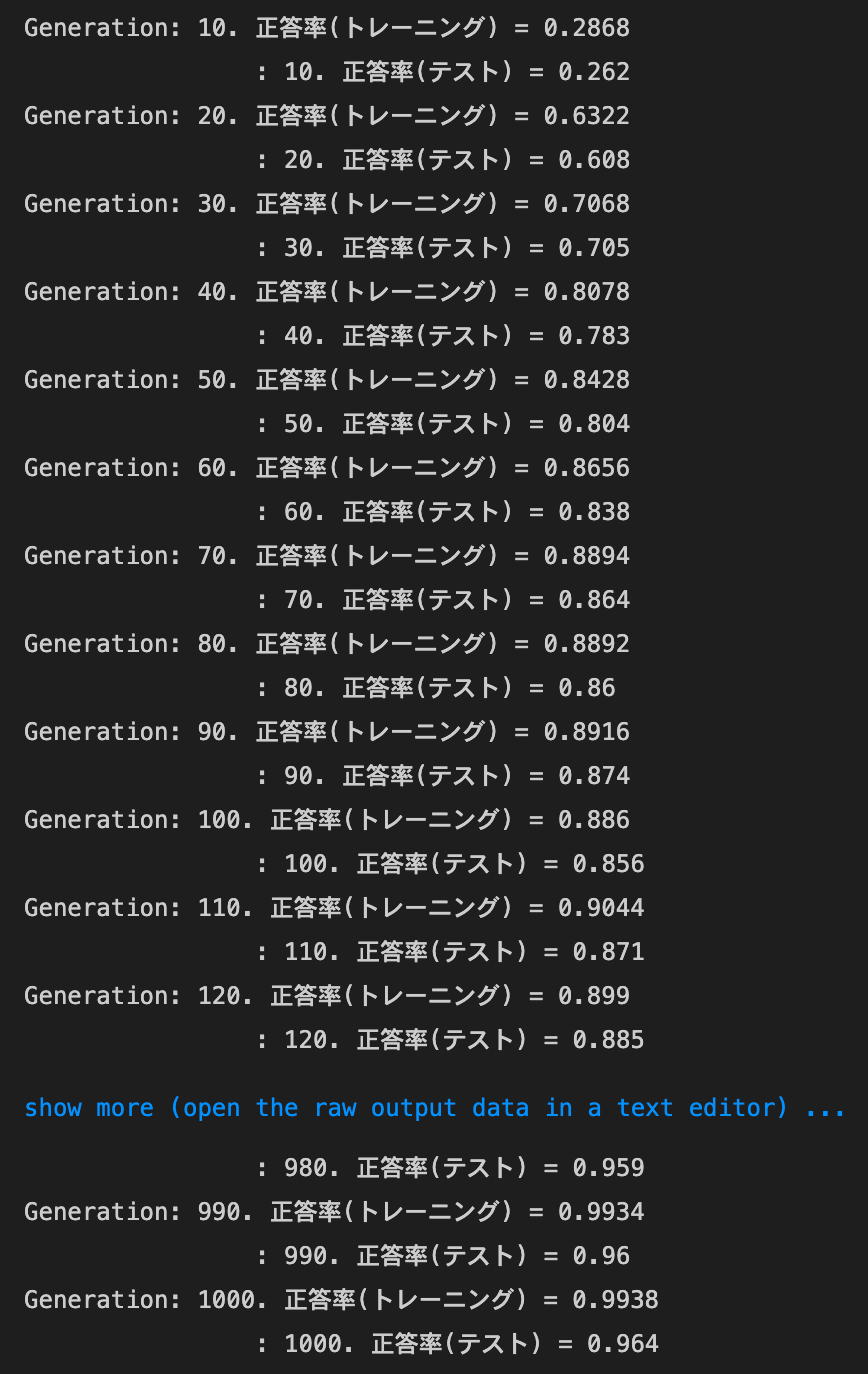
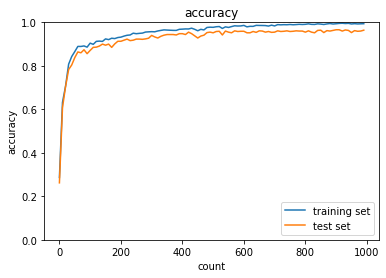
2_7_double_convolution_network_after.ipynb
実行結果

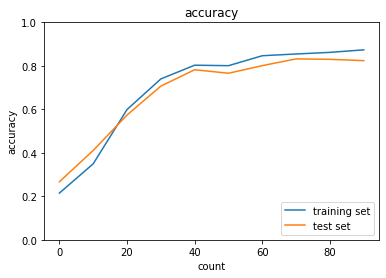
2_8_deep_convolution_net.ipynb
実行結果