【ラビット・チャレンジ】深層学習 後編 Day3
ラビット・チャレンジの受講レポート。
前回の復習
確認テスト
サイズ5×5の入力画像を、サイズ3×3のフィルタで畳み込んだときの出力画像のサイズは?
ストライドは2, パディングは1とする
【解答】
3×3
再帰型ニューラルネットワークについて
再帰型ニューラルネットワークの概念
RNN全体像
RNNとは
時系列データに対応可能なニューラルネットワーク
時系列データ
時間的順序を追って一定間隔ごとに観察され、
しかも相互に統計的依存関係が認められるようなデータの系列
例:
- 音声データ
- テキストデータ
RNNについて
全体像
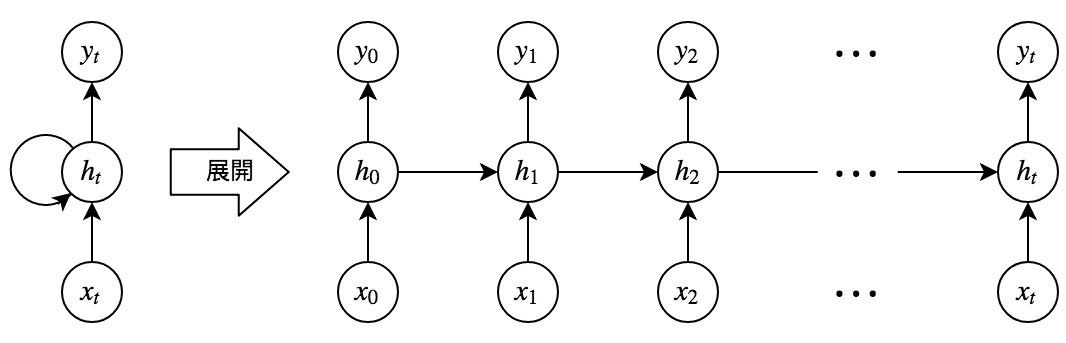
(画像:http://www.net.c.dendai.ac.jp/~ogata/)
「展開」の矢印の左右の図の意味は同じ

(画像:http://maruyama097.blogspot.com/2017/02/lstmrnn.html)
RNNの数学的記述
\[u^t = W_{(in)}x^t + W \overbrace{z^{t-1}}^{*1} + b \\ z^t = f(W_{(in)}x^t + Wz^{t-1} + b) \\ v^t = W_{(out)} z^t + c \\ y^t = g(W_{(out)} z^t + c) \\\] \[\begin{split} W_{(in)}: &入力層から中間層への重み \\ W_{(out)}: &中間層から出力層への重み \\ *1: &前の時間の中間層の出力 \end{split}\]活性化関数を通る前:$u / v$
活性化関数を通った後:$z / y$
入力側の矢印:$u, z$
出力側の矢印:$v, y$
u[:, t+1] = np.dot(X, W_in) + np.dot(z[:, t].reshape(1, -1), W)
z[:, t+1] = functions.sigmoid(u[:, t+1])
np.dot(z[:, t+1].reshape(1, -1), W_out) # vにあたる部分
y[:, t] = functions.sigmoid(np.dot(z[:, t+1].reshape(1, -1), W_out))
確認テスト
RNNのネットワークには大きく分けて3つの重みがある。
1つは入力から現在の中間層を定義する際にかけられる重み、
1つは中間層から出力を定義する際にかけられる重みである。
残り1つの重みについて説明せよ。
【解答】
中間層から中間層への重み
RNNの特徴
時系列モデルを扱うには、初期の状態と過去の時間t-1の状態を保持し、
そこから次の時間でのtを再帰的に求める再帰構造が必要
演習チャレンジ
以下は再帰型ニューラルネットワークにおいて構文木を入力とし再帰的に文全体の表現ベクトルを得るプログラム
ただし、ニューラルネットワークの重みパラメータはグローバル変数として定義してあるものとし、
_activation関数は何らかの活性化関数
木構造は再帰的な辞書で定義してあり、rootが最も外側の辞書であると仮定
(く)に当てはまるのは?
def traverse(node):
if not isinstance(node, dict):
v = node
else:
left = traverse(node['left'])
right = traverse(node['right'])
v = _activation(【(く)】)
return v
【解答】
W.dot(np.concatenate([left, right]))
→leftとrightの特徴量が失われないようにする
【補足】
concatenate: 配列を連結する処理- 連結したものに重みをかけることで、一旦大きくなった配列のサイズを元に戻す
- 構文木
- まず隣り合った単語同士の特徴量を抽出し、次にその隣り合った特徴量同士をあわせた特徴量を抽出し、それを繰り返して最終的に文全体を表す一つの特徴量を抽出する
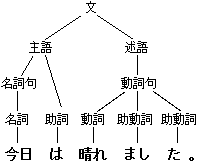
(画像:https://ja.wikipedia.org/wiki/%E6%A7%8B%E6%96%87%E6%9C%A8)
- まず隣り合った単語同士の特徴量を抽出し、次にその隣り合った特徴量同士をあわせた特徴量を抽出し、それを繰り返して最終的に文全体を表す一つの特徴量を抽出する
BPTT
BPTTとは
Back Propagation Through Time
逆誤差伝播法の復習
計算結果(=誤差)から微分を逆算
→不要な再帰的計算を避けて微分を算出
確認テスト
連鎖律の原理を使い、$\frac{dz}{dx}$を求めよ
\[z = t^2 \\ t = x + y\]【解答】
\[\frac{dz}{dx} = \frac{dz}{dt} \cdot \frac{dt}{dx} \\ \space \\ \Rightarrow \left\{ \begin{array}{ll} \frac{dz}{dt} = 2t \\ \frac{dt}{dx} = 1 \\ \end{array} \right. \\ \space \\ \begin{split} \Rightarrow \frac{dz}{dx} &= 2t \cdot 1 \\ &= 2(x + y) \end{split}\]BPTTの数学的記述
(本講座内で一番難しいところ!)
\[\frac{\partial E}{\partial W_{(in)}} = \frac{\partial E}{\partial u^t} \left[ \frac{\partial u^t}{\partial W_{(in)}} \right]^T = \delta^t[x^t]^T \\ \frac{\partial E}{\partial W_{(out)}} = \frac{\partial E}{\partial v^t} \left[ \frac{\partial v^t}{\partial W_{(out)}} \right]^T = \delta^{out, t}[z^t]^T \\ \frac{\partial E}{\partial W} = \frac{\partial E}{\partial u^t} \left[ \frac{\partial u^t}{\partial W} \right]^T = \delta^t[z^{t-1}]^T\] \[\frac{\partial E}{\partial b} = \frac{\partial E}{\partial u^t} \frac{\partial u^t}{\partial b} = \delta^t \\ \frac{\partial E}{\partial c} = \frac{\partial E}{\partial v^t} \frac{\partial v^t}{\partial c} = \delta^{out, t}\]RNNについてを参照しながら理解するとよい
重み$W_{(in)}$について (1つ目の式)
\[\frac{\partial E}{\partial W_{(in)}} = \frac{\partial E}{\partial u^t} \left[ \frac{\partial u^t}{\partial W_{(in)}} \right]^T = \delta^t[x^t]^T\]# コード例
np.dot(X.T, delta[:, t].reshape(1, -1))
より、$W_{(in)}$は$u^t$についての式
$\delta^t$: $E$を$u^t$まで微分したもの
$[ \space ]^T$: RNNにおいて、時間的に遡って微分を全部やる
重み$W_{(out)}$について (2つ目の式)
\[\frac{\partial E}{\partial W_{(out)}} = \frac{\partial E}{\partial v^t} \left[ \frac{\partial v^t}{\partial W_{(out)}} \right]^T = \delta^{out, t}[z^t]^T\]# コード例
np.dot(z[:, t+1].reshape(-1, 1), delta_out[:, t].reshape(-1, 1))
より、$W_{(out)}$は$v^t$についての式
$\delta^{out, t}$: $E$を$v^t$まで微分したもの
重み$W$について (3つ目の式)
\[\frac{\partial E}{\partial W} = \frac{\partial E}{\partial u^t} \left[ \frac{\partial u^t}{\partial W} \right]^T = \delta^t[z^{t-1}]^T\]# コード例
np.dot(z[:, t].reshape(-1, 1), delta[:, t].reshape(1, -1))
バイアス$b$について (4つ目の式)
\[\frac{\partial E}{\partial b} = \frac{\partial E}{\partial u^t} \frac{\partial u^t}{\partial b} = \delta^t \qquad \frac{\partial u^t}{\partial b} = 1\]バイアス$c$について (5つ目の式)
\[\frac{\partial E}{\partial c} = \frac{\partial E}{\partial v^t} \frac{\partial v^t}{\partial c} = \delta^{out, t} \qquad \frac{\partial v^t}{\partial c} = 1\]$\delta$について
\[\begin{split} \frac{\partial E}{\partial u^t} &= \frac{\partial E}{\partial v^t} \frac{\partial v^t}{\partial u^t} \\ &= \frac{\partial E}{\partial v^t} \frac{\partial\{W_{(out)}f(u^t) + c\}}{\partial u^t} \\ &= f'(u^t)W^T_{(out)} \delta^{out, t} \\ &= \delta^t \end{split}\]- $v^t = W_{(out)}z^t + c$, $z^t = f(u^t)$なので、$v^t = W_{(out)}f(u^t) + c$
- $\frac{\partial E}{\partial v^t} = \delta^{out, t}$
delta[:, t] = (np.dot(delta[:, t+1].T, W.T) + np.dot(delta_out[:, t].T, W_out.T)) * functions.d_sigmoid(u[:, t])
(ちなみに、、)
$\delta^t$と$\delta^{t-1}$の間には関係がある
$\delta^{t-z}$と$\delta^{t-z-1}$の間には関係がある
確認テスト
RNNの図において、$y_1$を$x, z_0, z_1, w_{in}, w, w_{out}$を用いて数式で表せ
※バイアスは任意の文字で定義
※中間層の出力にシグモイド関数$g(x)$を作用させよ
【解答】
\[z_1 = W_{in} x_1 + W z_0 + b \\ y_1 = g(W_{out} z_1 + c)\]パラメータの更新式
\[W^{t+1}_{(in)} = W^t_{(in)} - \epsilon \frac{\partial E}{\partial W_{(in)}} = W^t_{(in)} - \epsilon \sum_{z=0}^{Tt} \delta^{t-z}[x^{t-z}]^T \\ W^{t+1}_{(out)} = W^t_{(out)} - \epsilon \frac{\partial E}{\partial W_{(out)}} = W^t_{(out)} - \epsilon \delta^{out, t}[z^t]^T \\ W^{t+1} = W^t - \epsilon \frac{\partial E}{\partial W} = W^t - \epsilon \sum_{z=0}^{Tt} \delta^{t-z}[x^{t-z-1}]^T \\ b^{t+1} = b^t - \epsilon \frac{\partial E}{\partial b} = b^t - \epsilon \sum_{z=0}^{Tt} \delta^{t-z} \\ c^{t+1} = c^t - \epsilon \frac{\partial E}{\partial c} = c^t - \epsilon \delta^{out, t}\]$W_{(out)}$の処理では時間的に遡らない
中間層の前までは時間的な遡りを考慮する
$\epsilon$: 学習率
# コード例
W_in -= learning_rate * W_in_grad
# コード例
W_out -= learning_rate * W_out_grad
# コード例
W -= learning_rate * W_grad
BPTTの全体像
\[\begin{split} E^t &= loss(y^t, d^t) \\ &= loss \left( g(W_{(out)}z^t + c), d^t \right) \\ &= loss \left( g(W_{(out)}f( \underbrace{W_{(in)} x^t + Wz^{t-1} + b}_{*2} ) + c), d^t \right) \end{split}\]*2について
\[W_{(in)} x^t + Wz^{t-1} + b \\ W_{(in)} x^t + W f(u^{t-1}) + b \\ W_{(in)} x^t + W f(W_{(in)} x^{t-1} + Wz^{t-2} + b) + b\]コード演習問題
BPTTを行うプログラム
活性化関数は恒等関数
calculate_dout関数は損失関数を出力に関して偏微分した値を返す
(お)に当てはまるものは?
def bptt(xs, ys, W, U, V):
hiddens. outputs = rnn_net(xs, W, U, V)
dW = np.zeros_like(W)
dU = np.zeros_like(U)
dV = np.zeros_like(V)
do = _calculate_do(outputs, ys)
batch_size, n_seq = ys.shape[:2]
for t in reversed(range(n_seq)):
dV += np.dot(do[:, t].T, hiddens[:, t]) / batch_size
delta_t = do[:, t].dot(V)
for bptt_step in reversed(range(t+1)):
dW += np.dot(delta_t.T, xs[:, bptt_step]) / batch_size
dU += np.dot(delta_t.T, hiddens[:, bptt_step-1]) / batch_size
delta_t = 【(お)】
return dW, dU, dV
【解答】
delta_t.dot(U)
【解説】
RNNでは中間層出力$h_t$が過去の中間層出力$h_{t-1}, \cdots, h_1$に依存する
RNNにおいて喪失感すを重み$W$や$U$に関して偏微分するときは、これを考慮する必要があり
$\frac{dh_t}{dh_{t-1}} = U$
であることに注意すると、過去に遡るたびに$U$がかけられる
LSTM
- RNNの課題
- 時系列を遡るほど、勾配が消失していく
- 長い時系列の学習が困難
- 解決策
- 構造自体を変えて解決したのがLSTM
- 時系列を遡るほど、勾配が消失していく
確認テスト
シグモイド関数を微分したとき、入力値が0の時に最大値をとる
その値は?
【解答】
0.25
演習チャレンジ
RNNや深いモデルでは勾配の消失または爆発が起こる傾向にある
勾配爆発を防ぐために勾配のクリッピングを行うという手法がある
具体的には勾配のノルムがしきい値をこえたら
勾配のノルムをしきい値に正規化するというもの
以下は勾配のクリッピングを行う関数
(さ)に当てはまるのは?
def gradient_clipping(grad, threshold):
norm = np.linalg.norm(grad)
rate = threshold / norm
if rate < 1:
return 【(き)】
return grad
【解答】
gradient * rate
勾配 * (しきい値 / 勾配のノルム)と計算される
全体像
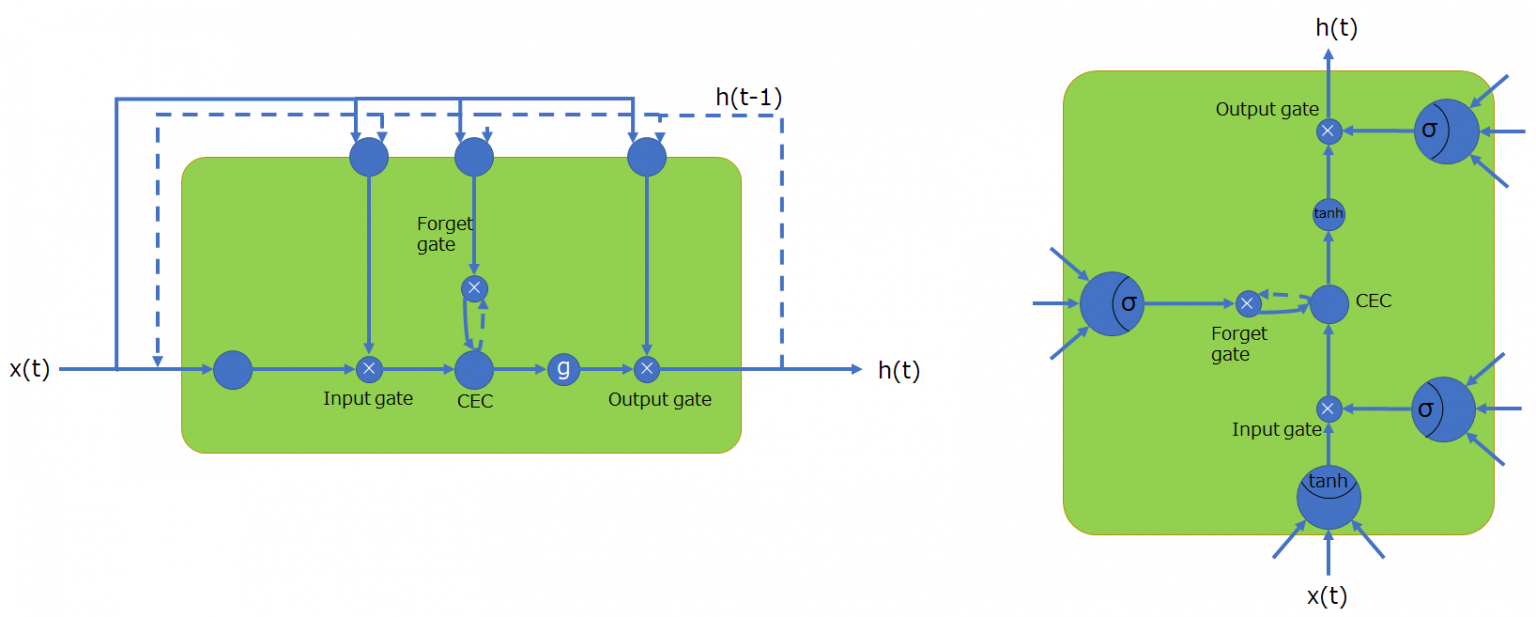
(画像:https://agirobots.com/lstmgruentrance-noformula/)
基本的にやっていることはRNNと同じ
点線(出力側→入力側)は時間的なループを表す
CECが大事
CEC
誤差カルーセル(Constant Error Caroucel)
記憶機能だけをもつ
勾配消失問題・勾配爆発問題:勾配が1であれば解決できる
課題
入力データについて、時間依存度に関係なく重みが一律
→NNの学習特性がない
→CECの前後に学習機能をもつものを置くことで対処
入力重み衝突:入力層→隠れ層の重み
出力重み衝突:隠れ層→出力層の重み
入力ゲートと出力ゲート
- 役割
- 入力ゲートと出力ゲートへの入力値の重みを、重み行列$W, U$で可変可能とする
- →CECの課題を解決
- 入力ゲート
- CECに対し、入力データを「こんなふうに」覚えてくださいね、と指示する
- 「こんなふうに」の部分、CECへの覚えさせ方をNNで学習
- 今回の入力値と前回の中間層からの出力値を元に、今回の入力データをどう記憶するか決める
- 今回の入力値に対する重み:$W_i$
- 前回の出力値に対する重み:$U_i$
- どれくらい覚えさせるか:$V_i c(t-1)$
- CECに対し、入力データを「こんなふうに」覚えてくださいね、と指示する
- 出力ゲート
- CECから取り出したデータを「こんなふうに」利用する、と決める
- 「こんなふうに」の部分をNNで学習
- 今回の入力値と前回の中間層からの出力値を元に、今回の記憶したデータをどう利用するか決める
- 今回の入力値に対する重み:$W_o$
- 前回の出力値に対する重み:$U_o$
- どれくらい利用するか:$V_o c(t)o(t)$
- CECから取り出したデータを「こんなふうに」利用する、と決める
忘却ゲート
過去の情報が要らなくなった場合、そのタイミングで情報を忘却させる
これがないと、不要になった情報が削除できない
→大昔の不要なデータが影響を与える可能性が出てしまう
確認テスト
以下の文章をLSTMに入力し、空欄に当てはまる単語を予測したい
文中の「とても」という言葉は空欄の予測において
なくなっても影響を及ぼさないと考えられる
この場合、どのゲートが作用する?
「映画おもしろかったね。ところで、とてもお腹が空いたから何か【空欄】。」
【解答】
忘却ゲート
演習チャレンジ
以下のプログラムはLSTMの順伝播を行うもの
ただし_sigmoid関数は要素ごとにシグモイド関数を作用させる
(け)に当てはまるのは?
def lstm(x, prev_h, prev_c, W, U, b):
# セルへの入力やゲートをまとめて計算し、分離
lstm_in = _activation(x.dot(W.T) + prev_h.dot(U.T) + b)
a, i, f, o = np.hsplit(lstm_in, 4)
# 値を変換、セルへの入力:(-1, 1) ゲート:(0, 1)
a = np.tanh(a)
input_gate = _sigmoid(i)
forget_gate = _sigmoid(f)
output_gate = _sigmoid(o)
# セルの状態を計算し、中間層の出力を計算
c = 【(け)】
h = output_gate * np.tanh(c)
return c, h
【解答】
input_gate * a + forget_gate * c
【解説】
新しいセルの状態 = 計算されたセルへの入力 * 入力ゲート + 1ステップ前のセルの状態 * 忘却ゲート
覗き穴結合
CEC自身の値に、重み行列を介して伝播可能にした構造
→CECの保存されている過去の情報を、
任意のタイミングで他のノードへ伝播させたり
任意のタイミングで忘却させたりしたい
→CEC自身の値は、ゲート制御に影響を与えていない
→CECの状態も判断材料に使ってみる
(あまり大きな改善はみられなかった)
GRU
パラメータを大幅に削減し、LSTMと同等またはそれ以上の精度が望めるようになった構造
→計算負荷が低い
(LSTMはパラメータ数が多く、計算負荷が高い)

(画像:https://ichi.pro/lstm-oyobi-gru-no-zukai-gaido-suteppubaisuteppu-no-setsumei-75771469479713)
隠れ層の状態:
\[h(t) = f \left( W_h x(t) + U_h \cdot (r(t) \cdot h(t-1)) b_h(t) \right)\]リセットゲート:
隠れ層をどのような状態で保持するかを制御
更新ゲート:
保持している値をどのように使って出力を得るか制御
隠れ層からの出力:
\[z(t) \cdot h(t-1) + (1-z(t)) \cdot h(t)\]確認テスト
LSTMとCECが抱える問題について、それぞれ簡潔に述べよ
【解答】
LSTM: パラメータが多いので、計算量が多い
CEC: 学習能力がない
演習チャレンジ
GRU(Gated Recurrent Unit)もLSTMと同様にRNNの一種であり、
単純なRNNにおいて問題となる勾配消失問題を解消し
長期的な依存関係を学習することができる。
LSTMに比べ変数の数やゲートの数が少なく、より単純なモデルであるが、
タスクによってはLSTMよりよい性能を発揮する
以下のプログラムはGRUの順伝播を行うプログラム
ただし_sigmoid関数は要素ごとにシグモイド関数を作用させる
(こ)にあてはまるのは?
def gru(x, h, W_r, U_r, W_z, U_z, W, U):
# ゲートを計算
r = _sigmoid(x.dot(W_r.T) + h.dot(U_r.T))
z = _sigmoid(x.dot(W_z.T) + h.dot(U_z.T))
# 次状態を計算
h_bar = np.tanh(x.dot(W.T) + (r * h).dot(U.T))
h_new = 【(こ)】
return h_new
【解答】
(1-z) * h + z * h_bar
【解説】
新しい中間状態は、1ステップ前の中間表現と計算された中間表現の線形和で表現される
確認テスト
LSTMとGRUの違いを簡潔に述べよ
【解答】
LSTMは入力ゲート、忘却ゲート、出力ゲートを用いて学習を行う
GRUはリセットゲートと更新ゲートを用いて学習を行う
LSTMにはCECがあるが、GRUにはない
LSTMはパラメータが多く、GRUは少ない
LSTMよりGRUの方が計算量が少ない
双方向RNN
過去の情報だけでなく、未来の情報を加味することで
精度を向上させるためのモデル

(画像:https://cvml-expertguide.net/2020/05/17/rnn/)
実用例:
- 文章の推敲
- 機械翻訳
演習チャレンジ
以下は双方向RNNの順伝播を行うプログラム
順方向については入力から中間層への重みW_f
一ステップ前の中間層出力から中間層への重みをU_f
逆方向に関しては同様にパラメータW_b, U_bをもち、
両者の中間層表現をあわせた特徴から出力層への重みはVである
_rnn関数はRNNの順伝播を表し中間層の系列を返す関数
(か)にあてはまるのは?
def bidirectional_rnn_net(xs, W_f, U_f, W_b, U_b, V):
xs_f = np.zeros_like(xs)
xs_b = np.zeros_like(xs)
for i. x in enumerate(xs):
xs_f[i] = x
xs_b[i] = x[::-1]
hs_f = _rnn(xs_f, W_f, U_f)
hs_b = _rnn(xs_b, W_b, U_b)
hs = 【(か)】
ys = hs.dot(V.T)
return ys
【解答】
np.concatenate([h_f, h_b[::-1]], axis=1)
【解説】
双方向RNNでは、順方向と逆方向に伝播したときの中間層表現をあわせたものが特徴量となる
(横方向に連結するのではなく、縦方向に連結。同じ時間のデータを組にする)
RNNでの自然言語処理
Seq2Seq
Encoder-Decoderモデルの一種
実用例:
- 機械対話
- 機械翻訳
全体像
(画像:https://twitter.com/yagami_360/status/942065105461637121?lang=ja)
Encoder RNN
ユーザがinputしたテキストデータを、
単語等のトークンに区切って渡す構造
- Taking
- 文章をトークン毎に分割し、トークン毎のIDに分割する
- 各単語をone-hotベクトルで表す (ベクトルの大きさは万単位)
- 文章をトークン毎に分割し、トークン毎のIDに分割する
- Embedding
- IDから、そのトークンを表す分散表現ベクトルに変換する
- 学習で200~300程度の大きさのベクトルにする
- 意味の近いものをまとめる
- IDから、そのトークンを表す分散表現ベクトルに変換する
- Encoder RNN
- ベクトルを順番にRNNへ入力していく
- vec1をRNNへ入力し、hidden stateを出力
- このhidden stateと次の入力vec2をまたRNNへ入力してhidden stateを出力。以降繰り返す
- 最後のvecを入れたときのhidden stateをfinal stateとする
- final state = thought vector(文脈ベクトル)
- 入力した文の意味を表すベクトル
- final state = thought vector(文脈ベクトル)
- vec1をRNNへ入力し、hidden stateを出力
- ベクトルを順番にRNNへ入力していく
- BERT
- by Google
- 特徴量抽出で良い成績
- MLM(Masked Language Model)
- 文の一部を隠し、前後の文脈からその部分を予測
Decoder RNN
システムがアウトプットデータを
単語等のトークンごとに生成する構造
- Decoder RNN
- Encoder RNNのfinal stateから、各トークンの生成確率を出力
- final stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力
- Encoder RNNのfinal stateから、各トークンの生成確率を出力
- Sampling
- 生成確率に基づいてtokenをランダムに選ぶ
- Embedding
- Samplingで選ばれたtokenをEmbeddingしてDecoder RNNへの次の入力とする
- Detokenize
- 上記をくり返し、Samplingで得られたtokenを文字列に直す
確認テスト
seq2seqの説明として正しいものは?
【解答】
RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる
演習チャレンジ
機械翻訳タスクにおいて、入力は複数の単語からなる文(文章)であり、
それぞれの単語はone-hotベクトルで表現されている
Encoderにおいて、それらの単語は単語埋め込みにより特徴量に変換され、
そこからRNNによって(一般にはLSTMを使うことが多い)
時系列の情報をもつ特徴へとエンコードされる
以下は、入力である文を時系列の情報をもつ特徴量へとエンコードする関数
ただし、_activation関数は何らかの活性化関数
(き)にあてはまるのは?
def encode(words, E, W, U, b):
hidden_size = W.shape[0]
h = np.zeros(hidden_size)
for w in words:
e = 【(き)】
h = _activation(W.dot(e) + U.dot(h) + b)
return h
【解答】
E.dot(w)
【解説】
単語wはone-hotベクトル
これを単語埋め込みにより別の特徴量へ変換する
HRED
過去n-1個の発話から次の発話を生成する
→より人間らしい文章が生成される
Seq2Seqの課題を解決
→一問一答しかできない
→問に対して文脈も何もなく、ただ応答が行われ続ける

(画像:https://khide-en.hatenablog.com/entry/2018/02/25/150000)
Seq2Seq + Context RNN
Context RNN: Encoderのまとめた各文章の系列をまとめて、
これまでの会話コンテキスト全体を表すベクトルに変換する構造
→過去の発話の履歴を加味した返答が可能
課題:
- 確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がない
- 同じコンテキストを与えられても、答えの内容が毎回会話の流れとしては同じものしか出せない
- 短く情報量に乏しい答えをしがち
- 短くてよくある答えを学ぶ傾向
- 「うん」「そうだね」など
- 短くてよくある答えを学ぶ傾向
VHRED
HREDにVAEの潜在変数の概念を追加したもの
VAEの潜在変数の概念を追加することで、HREDの課題を解決
VAE
オートエンコーダー
教師なし学習
具体例:
28*28の数字の画像を入力し、同じ画像を出力するNN (MNISTの場合)
構造:
Encoder: 入力データから潜在変数zに変換するNN
Decoder: 逆に潜在変数zをインプットとして元画像を復元するNN
メリット:
次元削減が行える
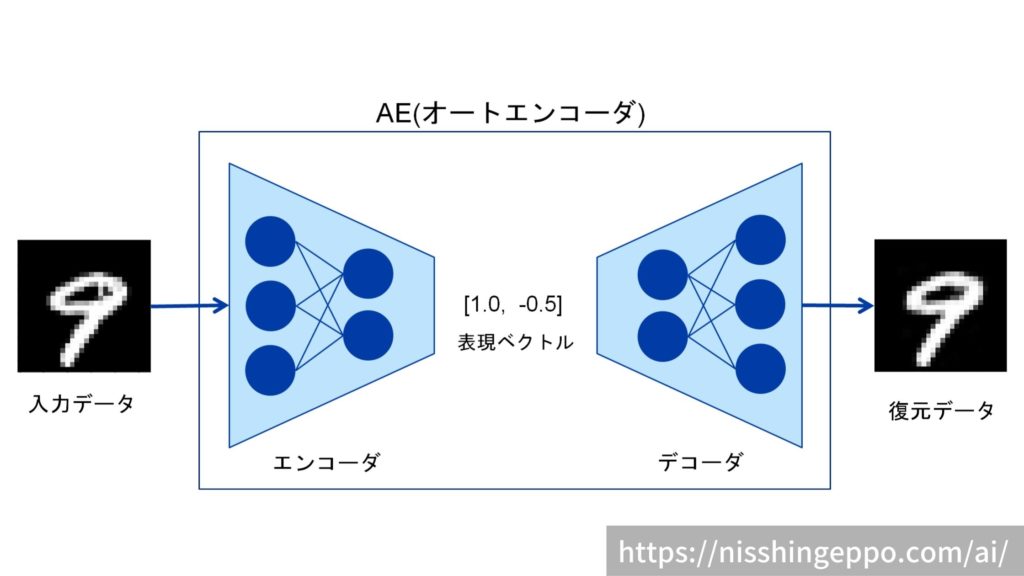
(画像:https://nisshingeppo.com/ai/whats-autoencorder/)
VAE
潜在変数zに確率分布z-N(0, 1)を仮定したもの
データを潜在変数zの確率分布という構造に押し込めることを可能にする
(普通のオートエンコーダの場合、潜在変数zに押し込めたデータの構造がどのような状態かわからない)
Word2Vec
one-hotベクトルからEmbeddingを得るためのもの
学習データからボキャブラリを作成
RNNの課題
→単語のような可変長の文字列をNNに与えられない
→固定長形式で単語を表す必要あり
メリット:
大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした
→ボキャブラリ * 任意の単語ベクトル次元で重み行列が誕生
Attention Mechanism
「入力と出力のどの単語が関連しているのか」
の関連度を学習する仕組み
Seq2Seqの課題:
長い文章への対応が難しい
→何単語でも(文の長さに関わらず)、固定次元ベクトルの中に入力しなくてはならない
解決策:
文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく仕組み
確認テスト
RNNとword2vec, seq2seqとAttentionの違いを簡潔に述べよ
【自分の解答】
- RNNは可変長の文字列をNNに与えられないが、Word2Vecではボキャブラリx任意の単語ベクトル次元で重み行列ができる
- Seq2Seqは単語数に関わらず固定次元ベクトルの中に入力する必要があり長い文章への対応が難しいが、Attentionは文章の長さに応じてシーケンスの内部表現の次元も大きくなる
【模範解答】
- RNN: 時系列データを処理するのに適したネットワーク
- Word2Vec: 単語の分散表現ベクトルを得る手法
- Seq2Seq: 一つの時系列データから別の時系列データを得るネットワーク
- Attention: 時系列データの中身の関連性に重みをつける手法
確認テスト
seq2seqとHRED, HREDとVHREDの違いを簡潔に述べよ
【解答】
- seq2seq: 一問一答、ある時系列データから別の時系列データを作り出す
- HRED: 文脈の意味ベクトルを加えられるようにすることで、文脈の意味を汲み取った変換を可能にしたもの
- VHRED: VAEの機構を取り入れることで、文脈に対して当たり障りのない解答以上の出力ができるように改良されたもの
実装演習
3_1_simple_RNN_after.ipynb
-
実行結果
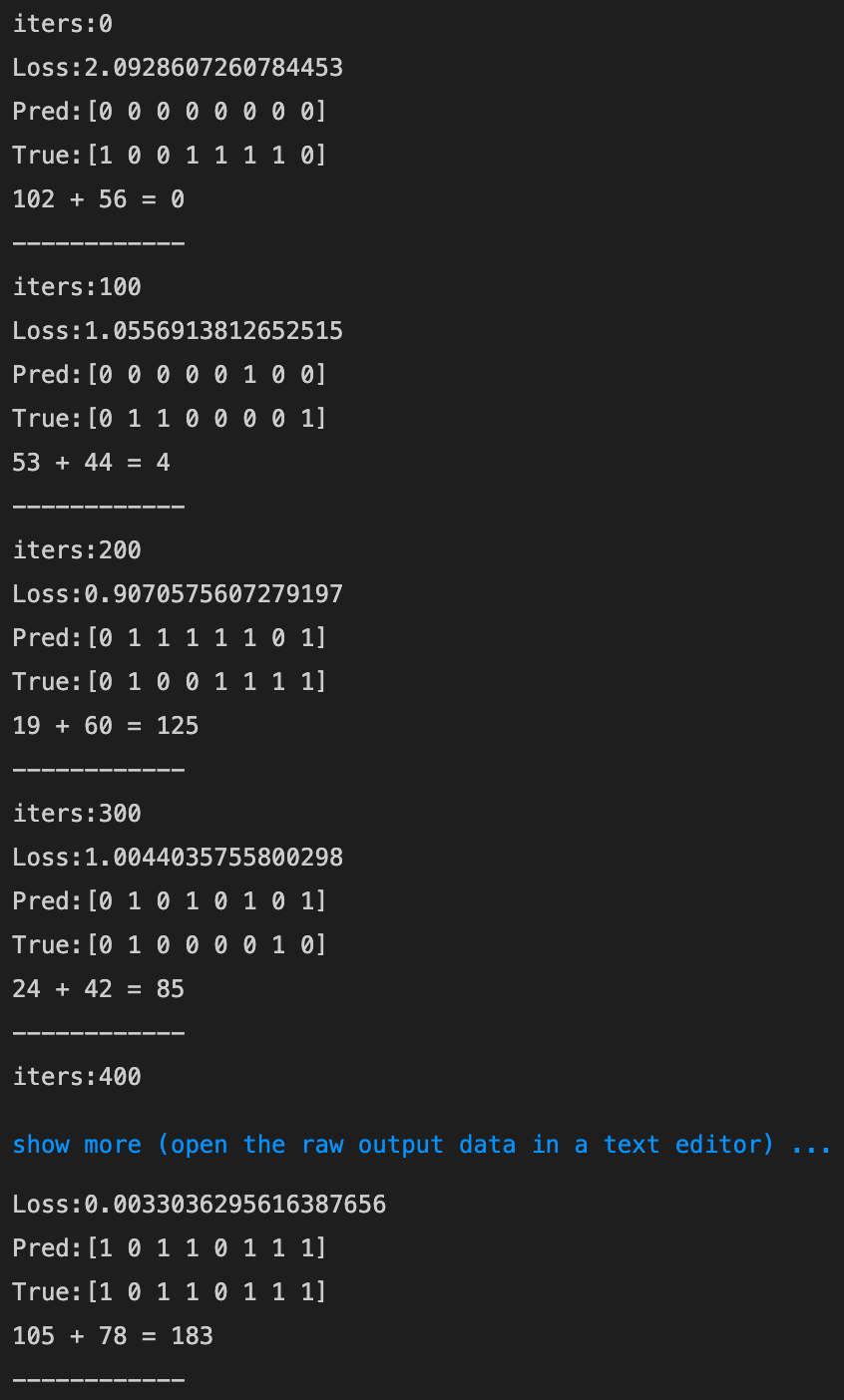
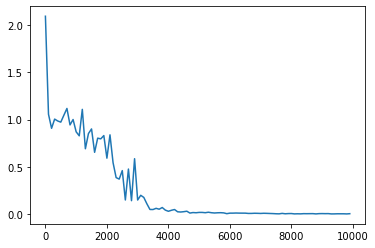
- [try] weight_init_stdやlearning_rate, hidden_layer_sizeを変更してみる
- weight_init_stdを変更
- 1→0.1にしてみる
- 発散してしまった
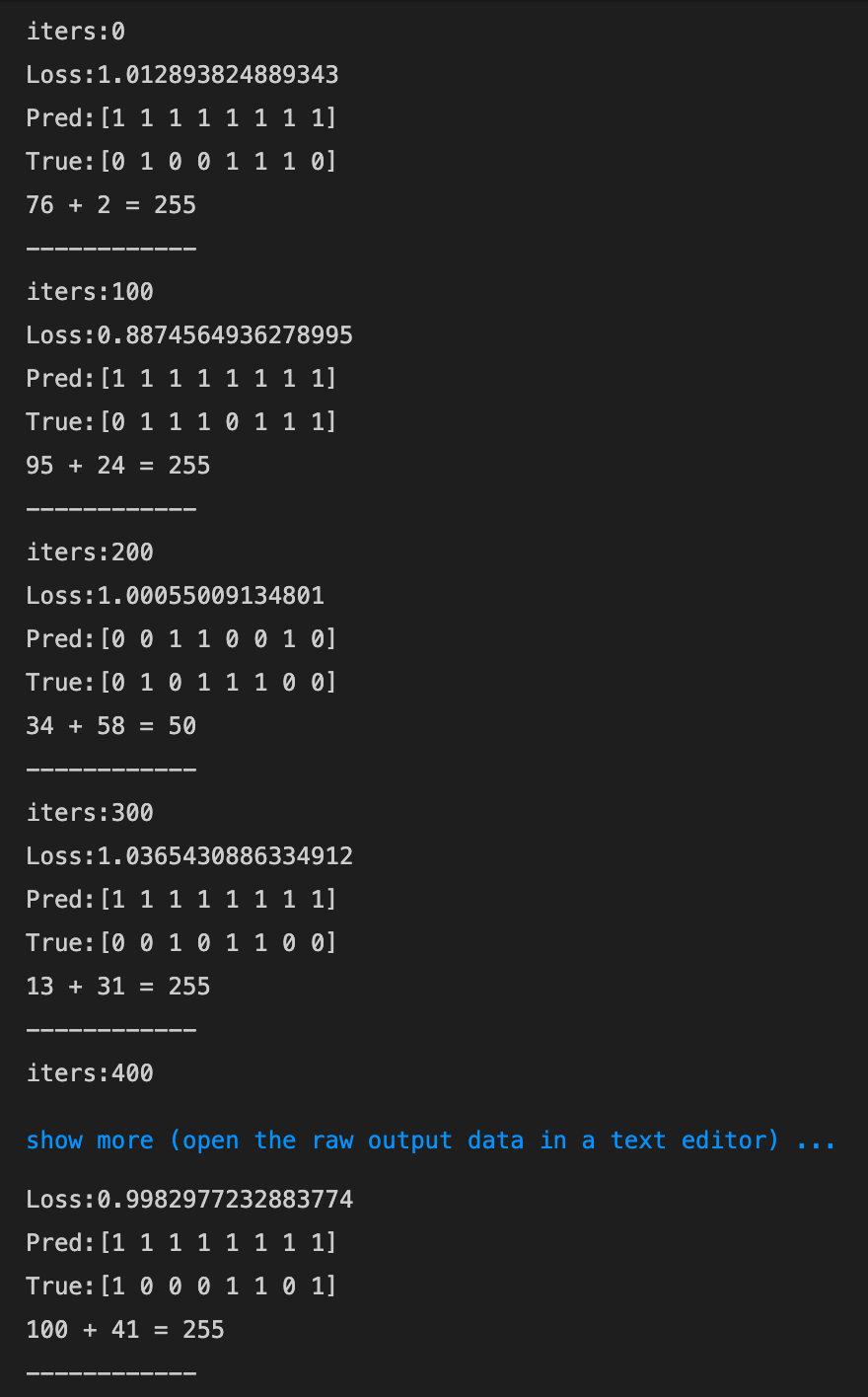
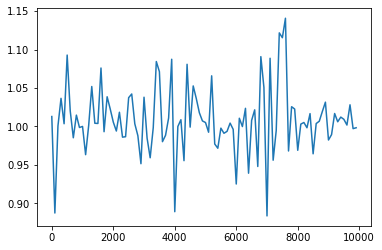
- 発散してしまった
- 1→0.9にしてみる
- 6000回を超えたあたりから収束
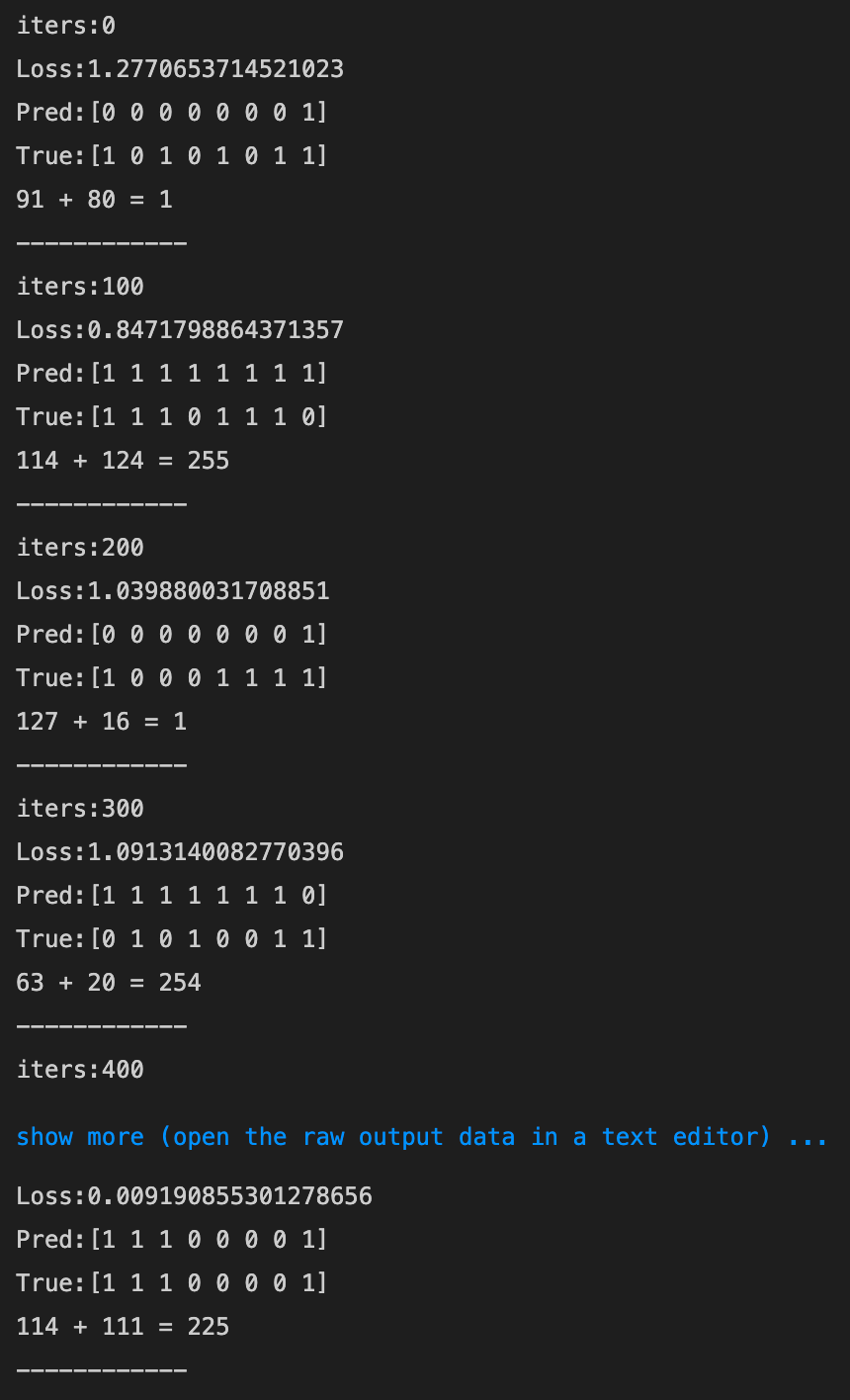
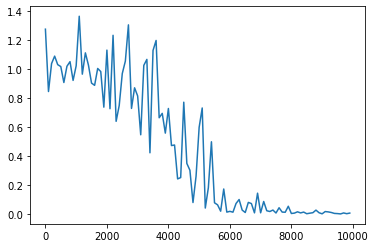
- 6000回を超えたあたりから収束
- 1→3にしてみる
- 6000回あたりまで収束傾向にあったが、その後少し発散気味
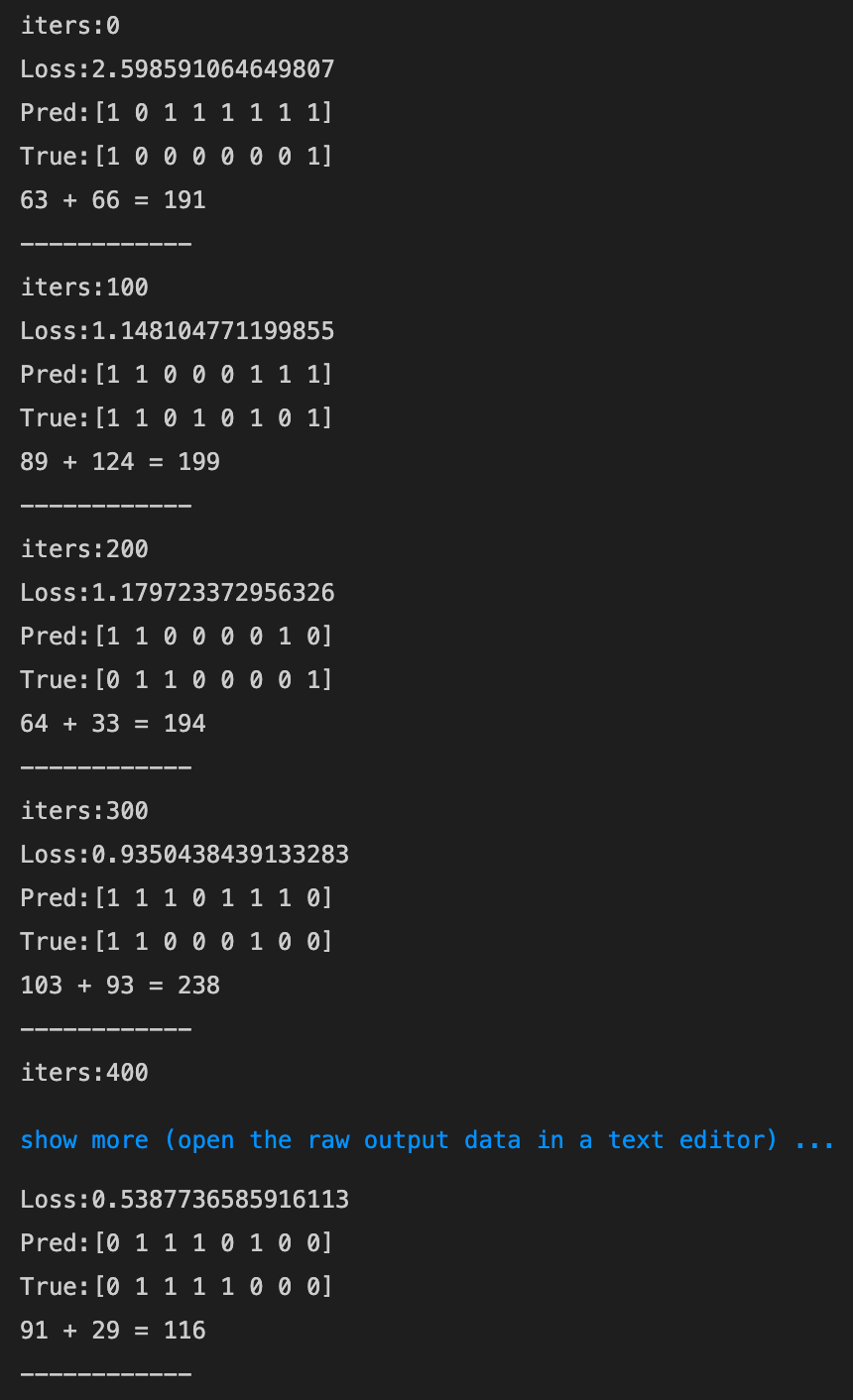
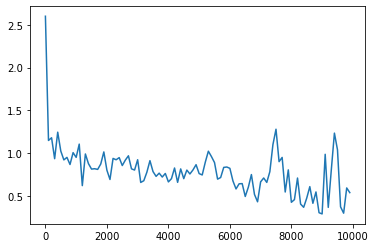
- 6000回あたりまで収束傾向にあったが、その後少し発散気味
- 1→0.1にしてみる
- learning_rateを変更してみる
- 0.1→0.5にしてみる
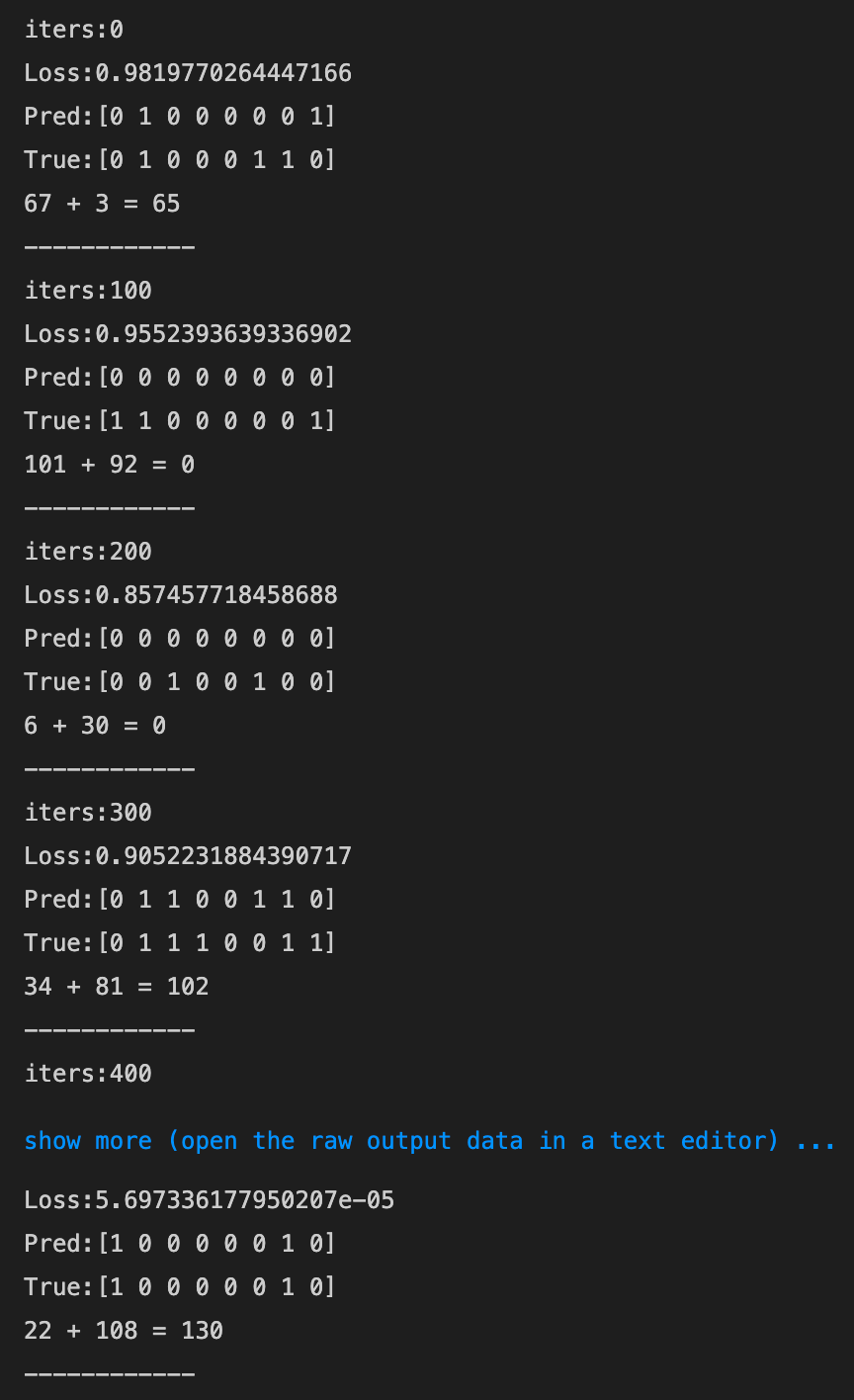
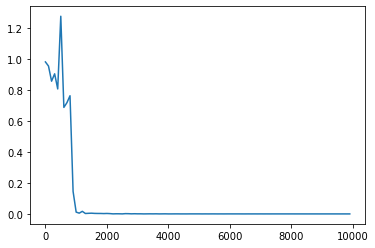
- 0.1→0.01にしてみる
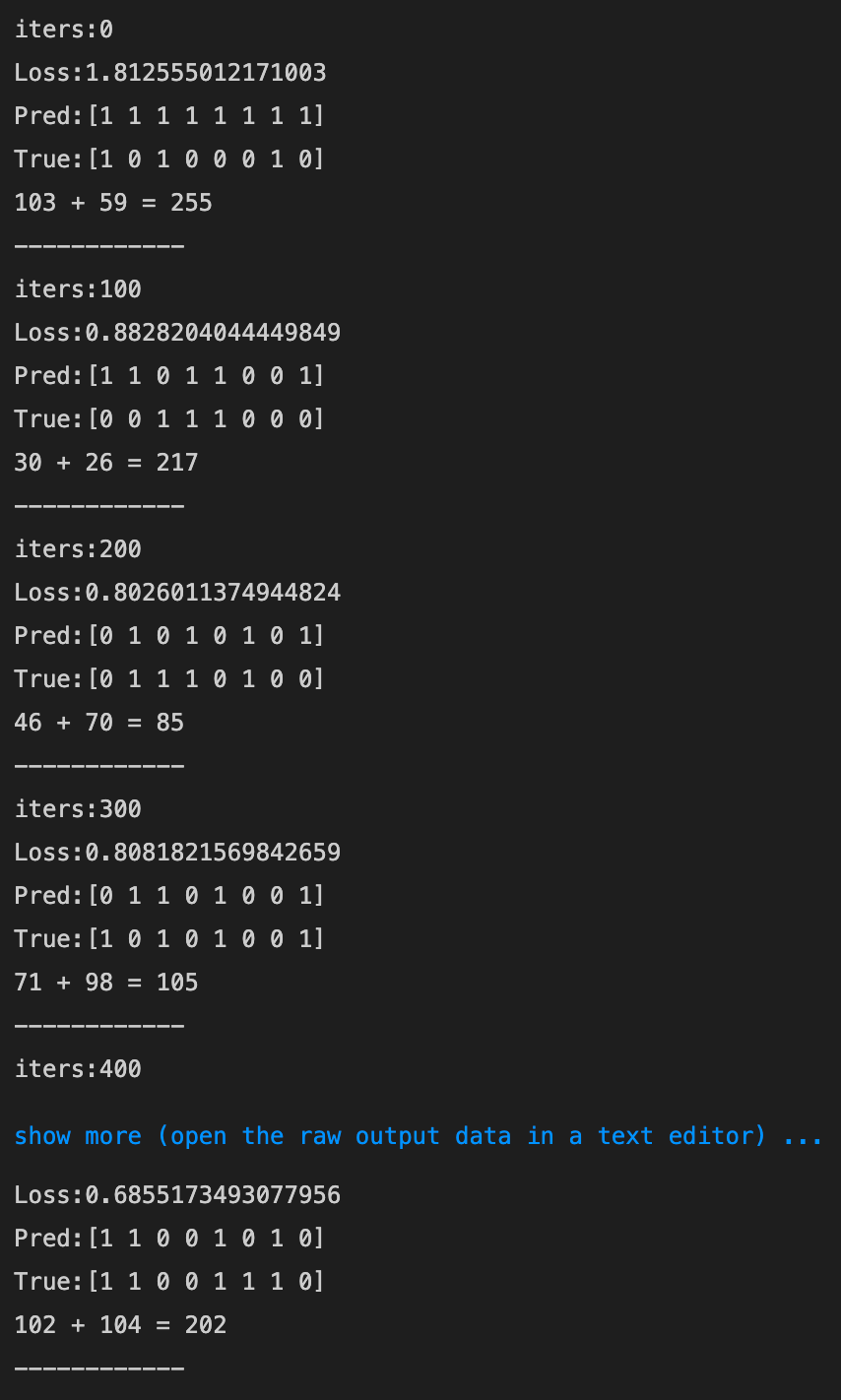
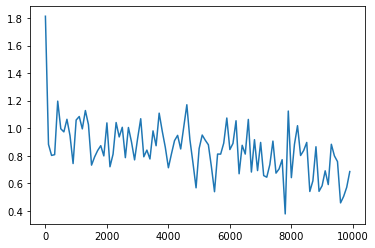
- 0.1→0.5にしてみる
- hidden_layer_sizeを変更してみる
- 16→80にしてみる
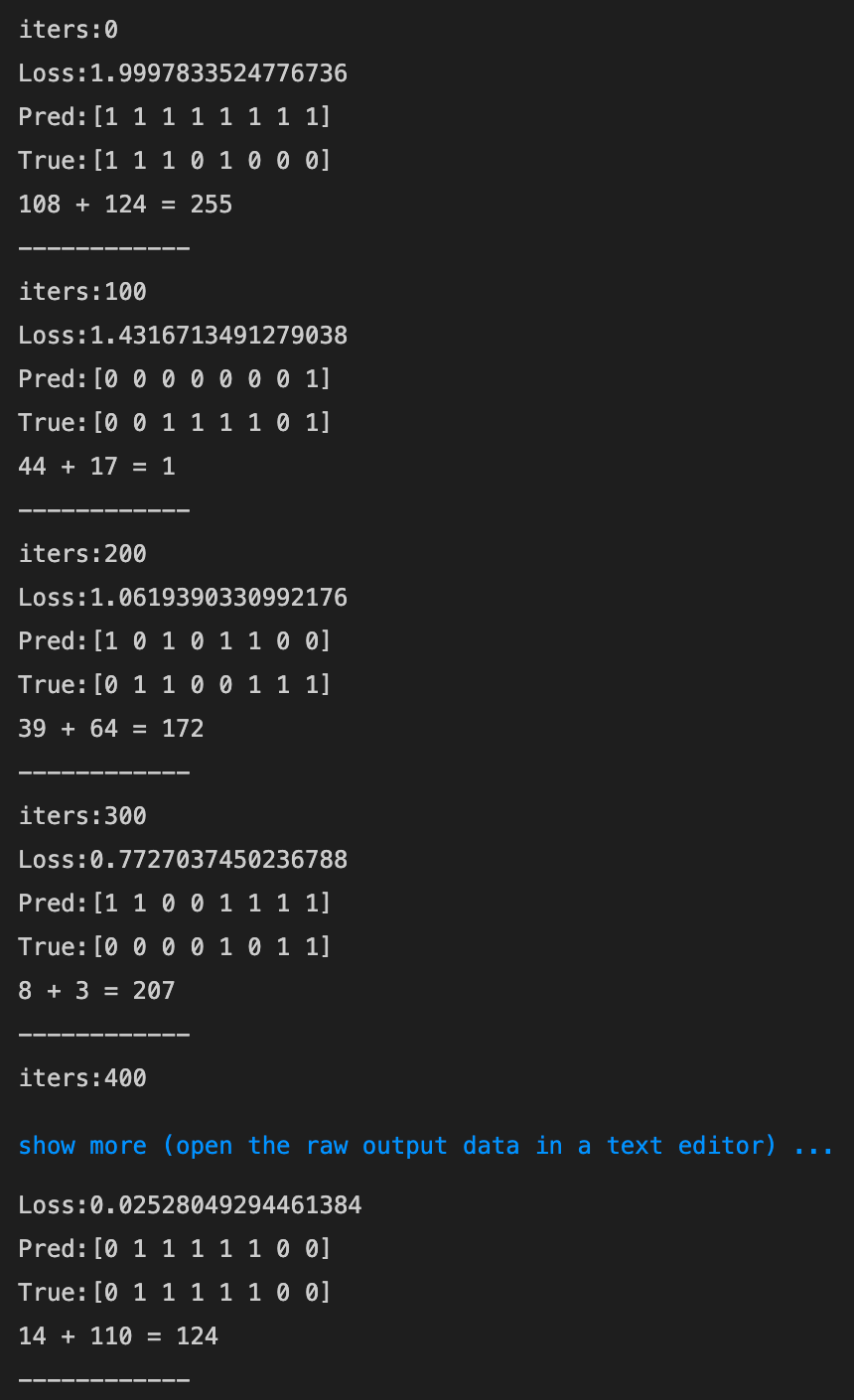
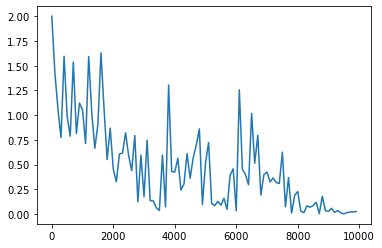
- 16→8にしてみる
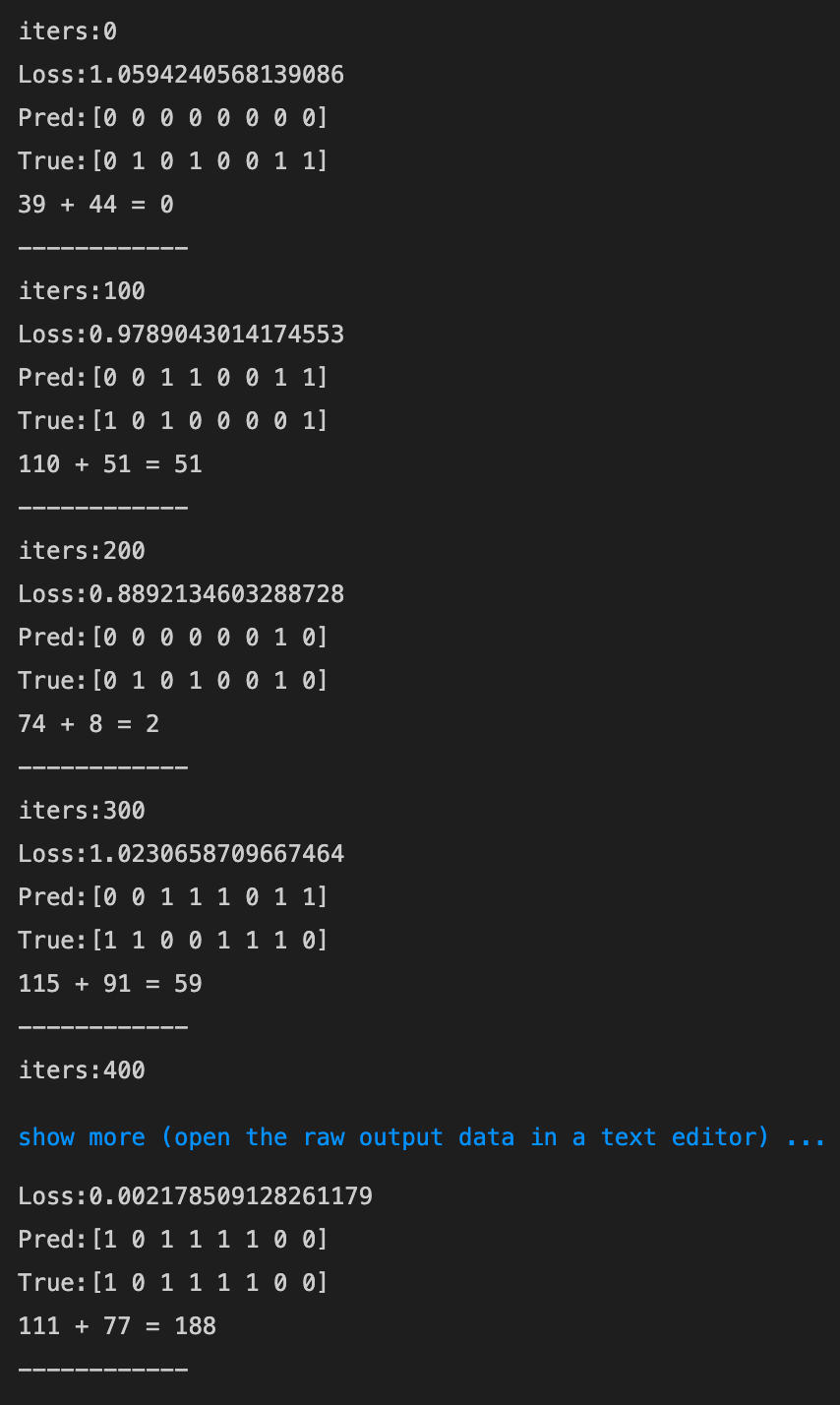
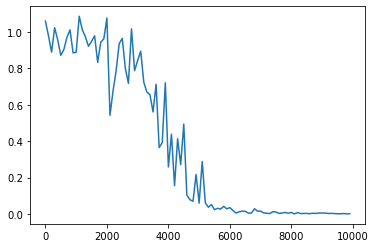
- 16→80にしてみる
- weight_init_stdを変更
- [try] 重みの初期化方法を変更してみる
- Xavier
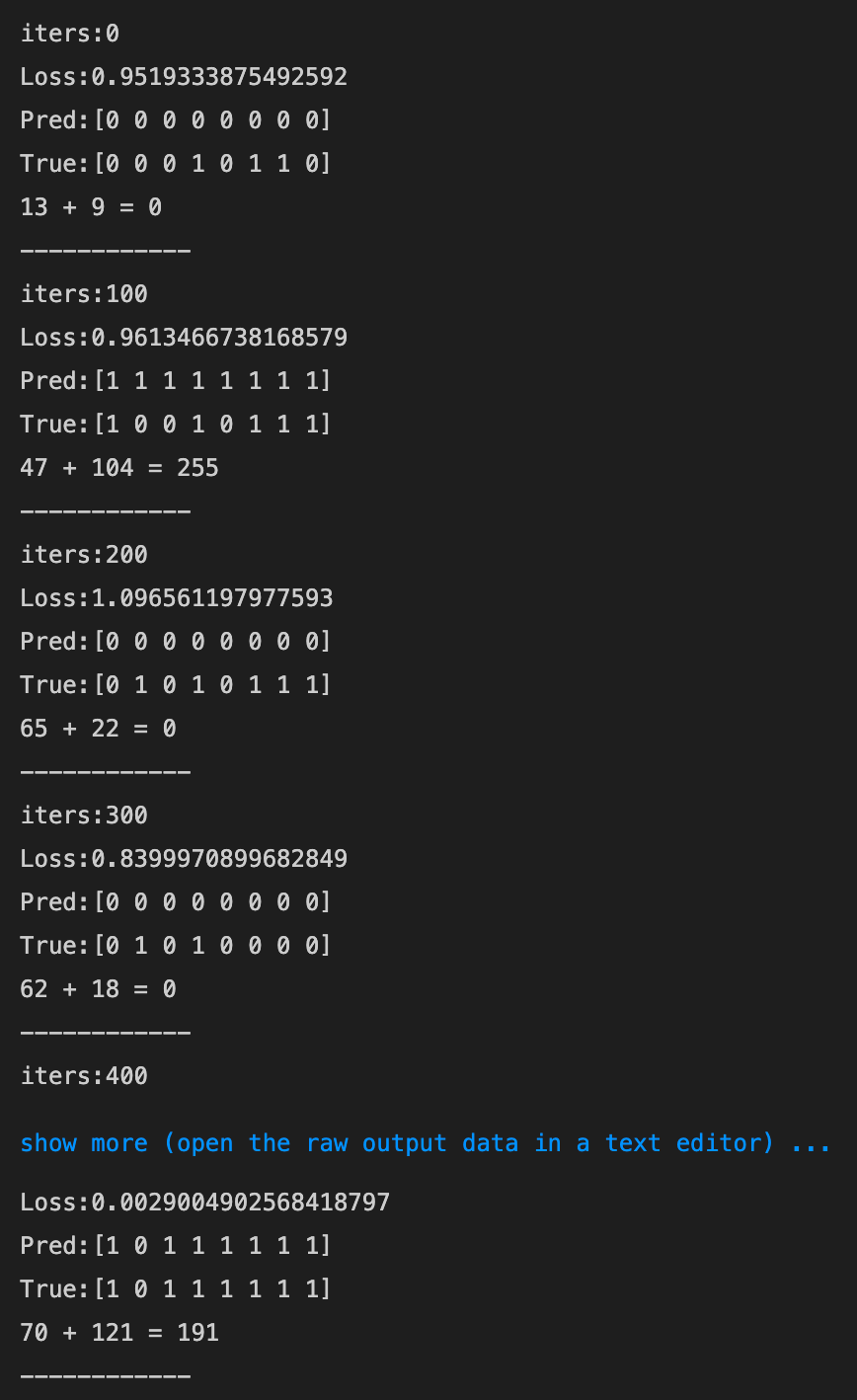
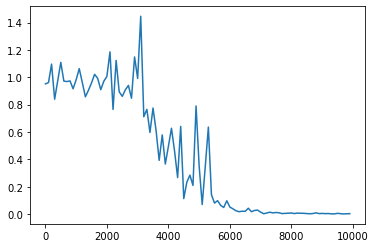
- He
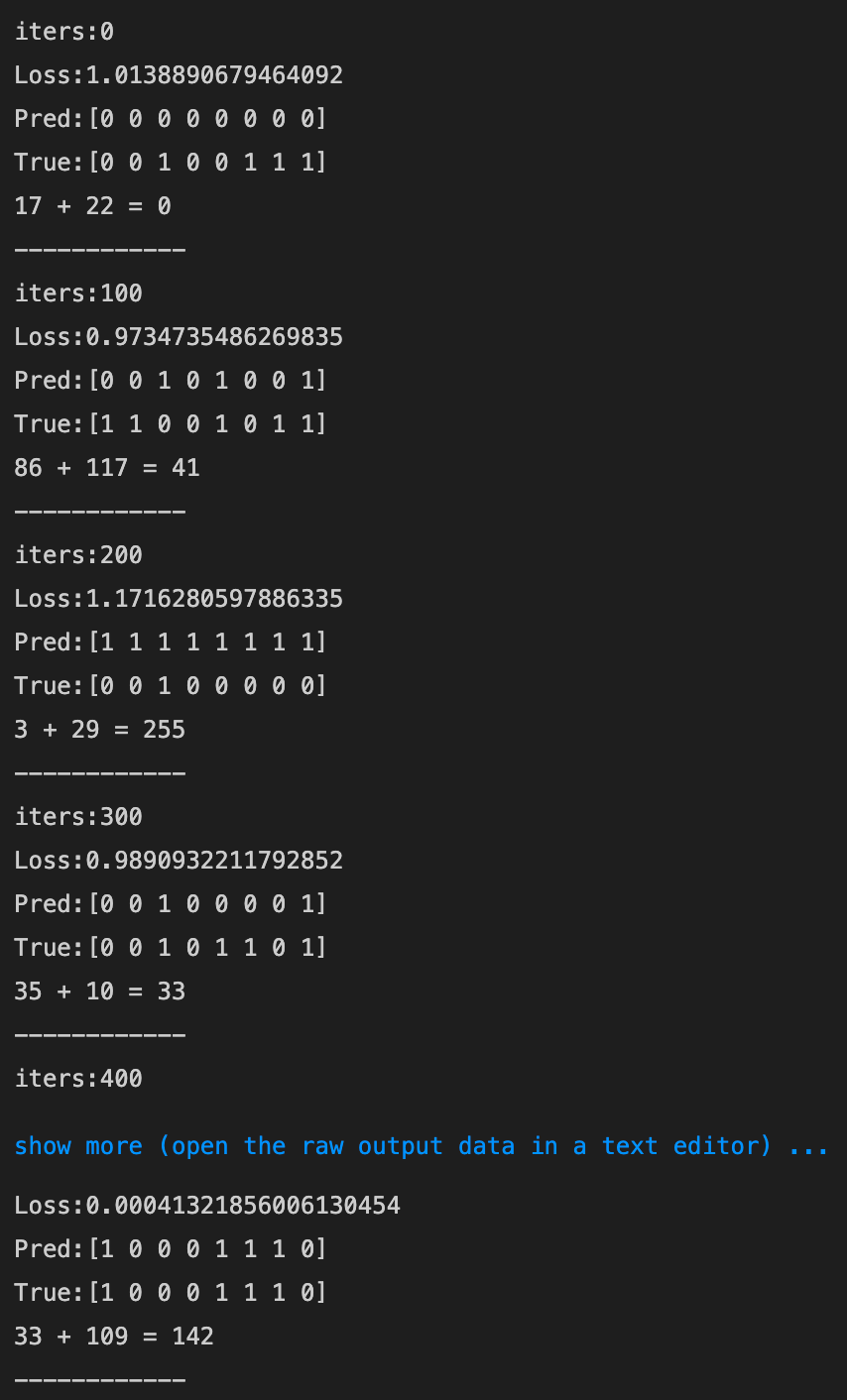
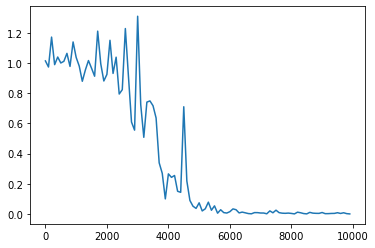
- Xavier
- [try] 中間層の活性化関数を変更してみる
- ReLU(勾配爆発を確認しよう)
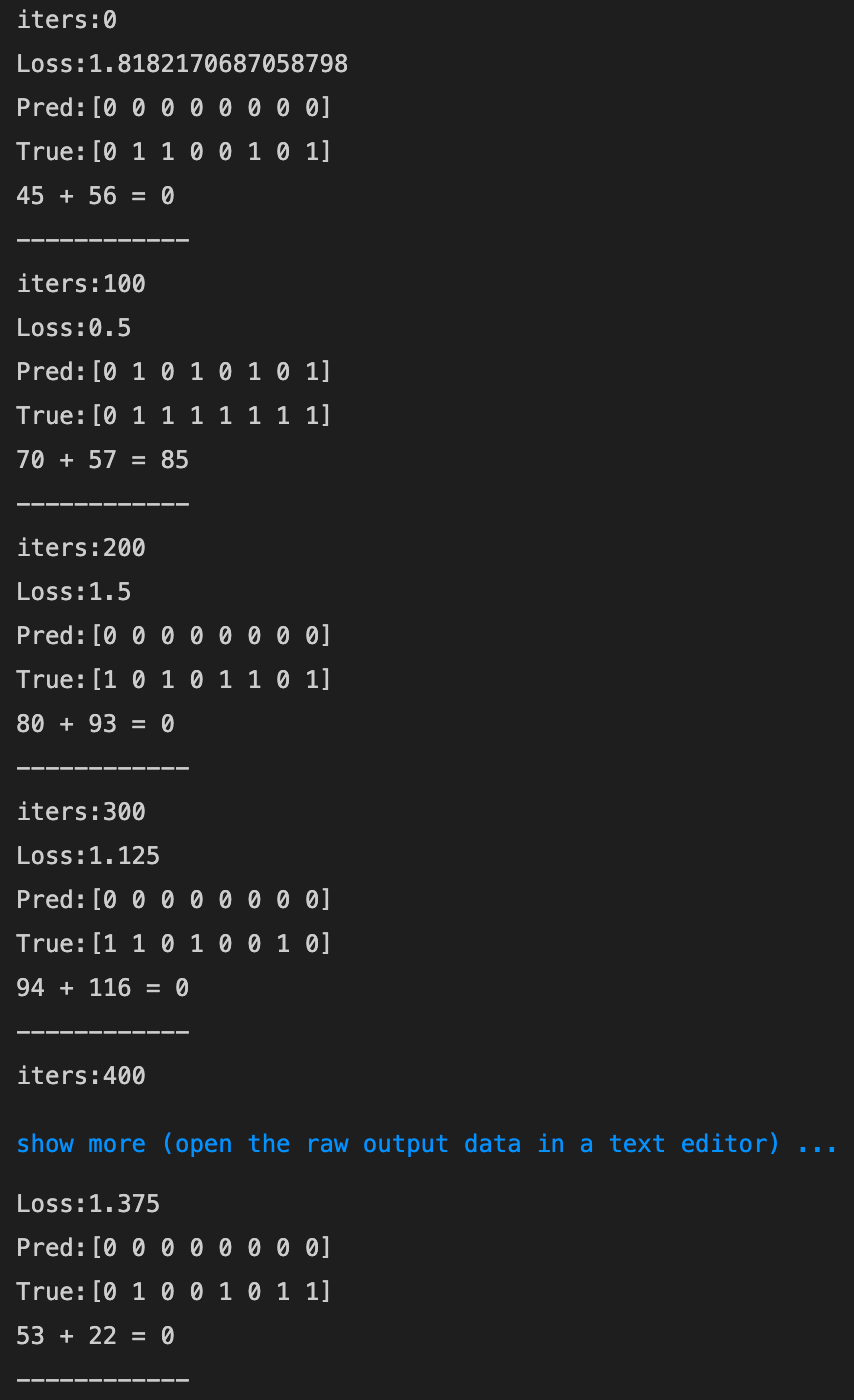
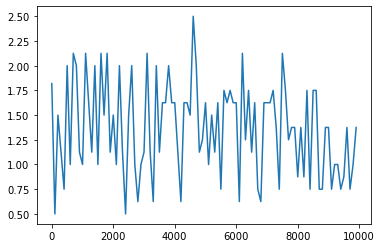
- tanh(numpyにtanhが用意されている。導関数をd_tanhとして作成しよう)
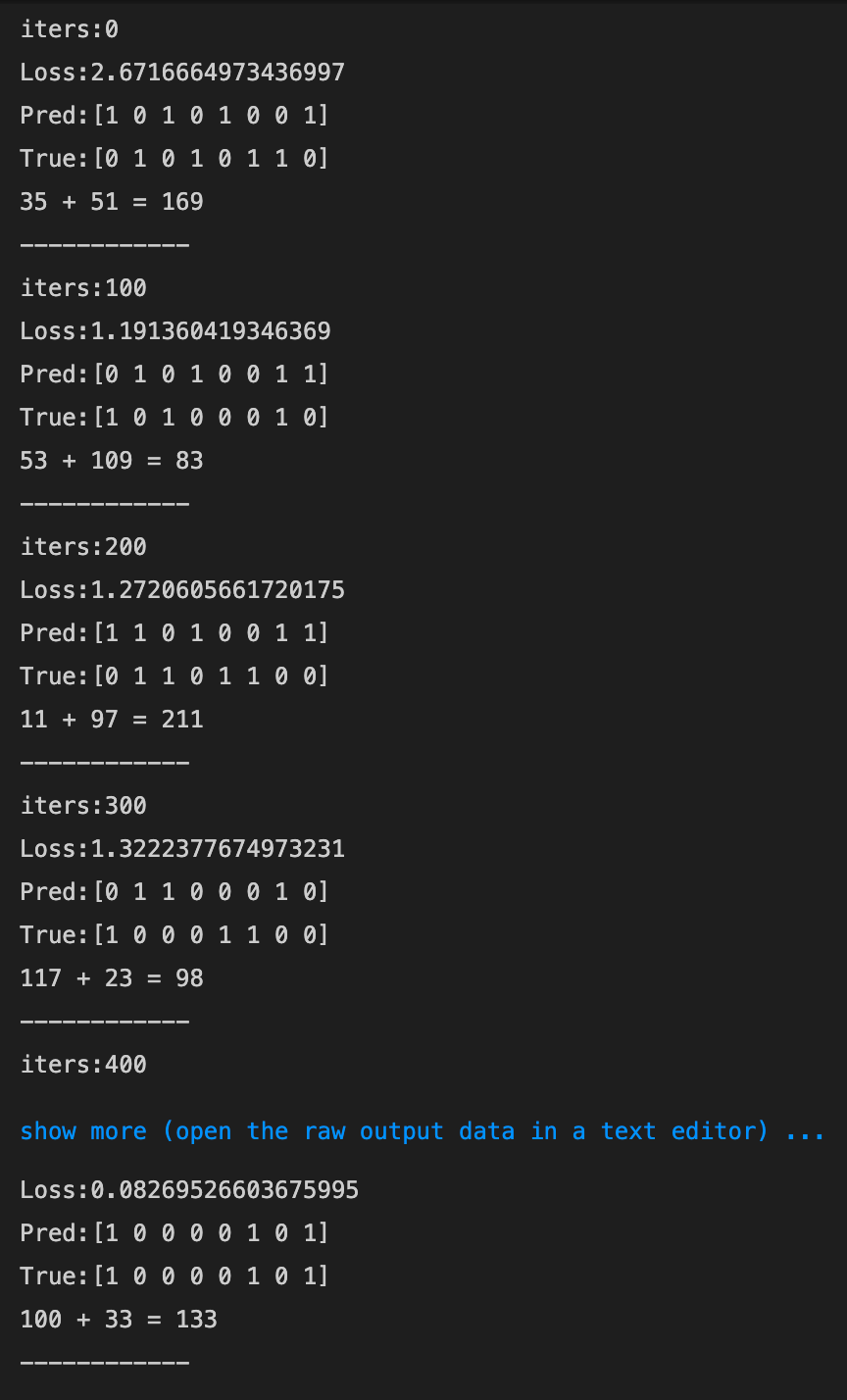
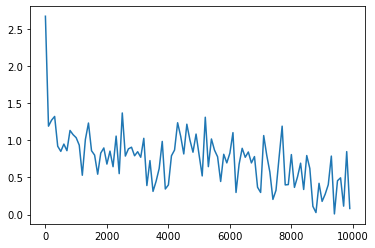
- ReLU(勾配爆発を確認しよう)
predict_word.ipynb
実行結果
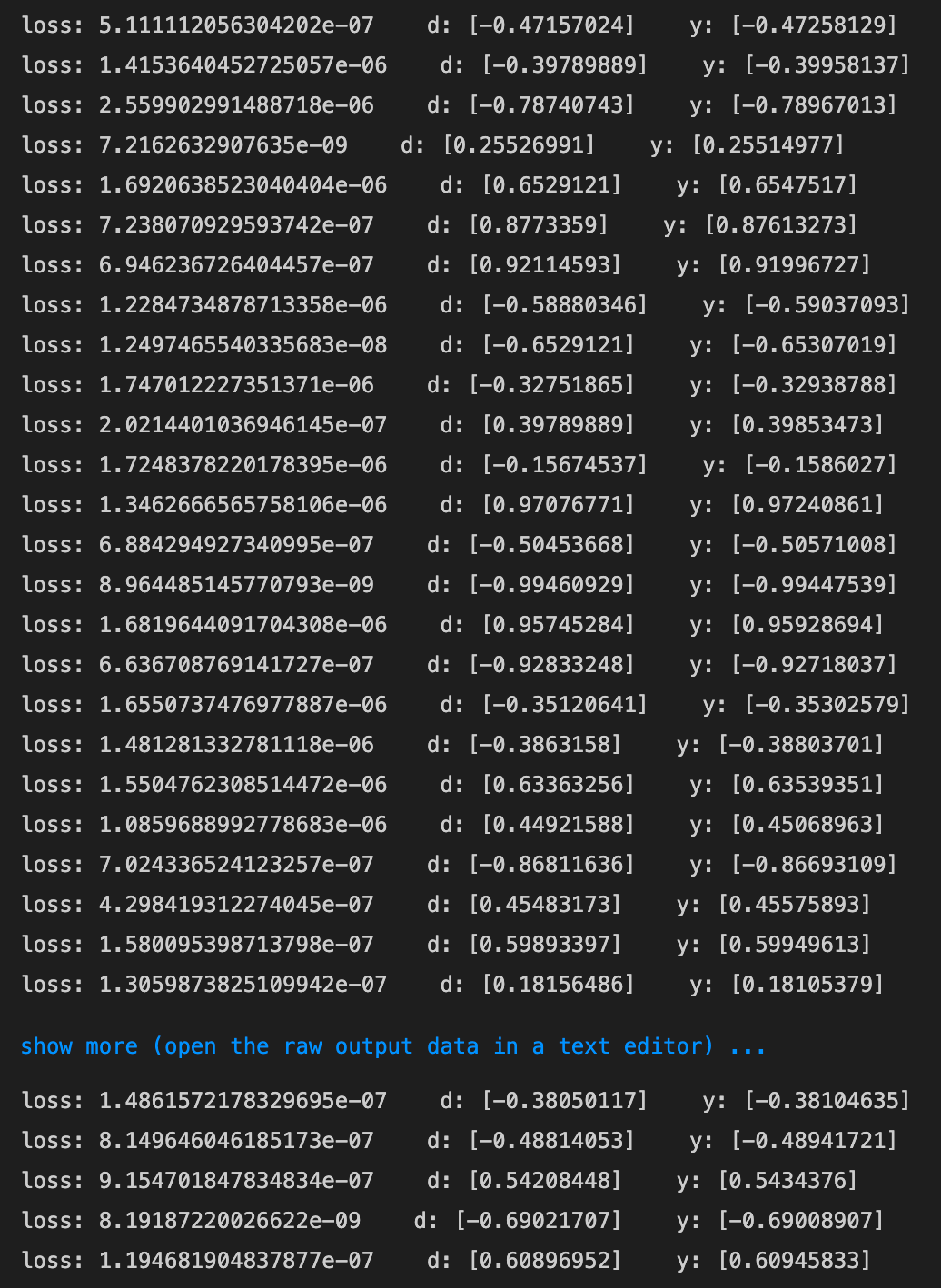
3_3_predict_sin.ipynb
- 実行結果
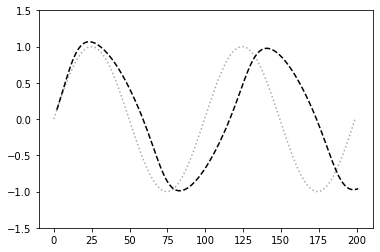
- [try] iters_numを100にする
- 振幅が0に近づいてしまった
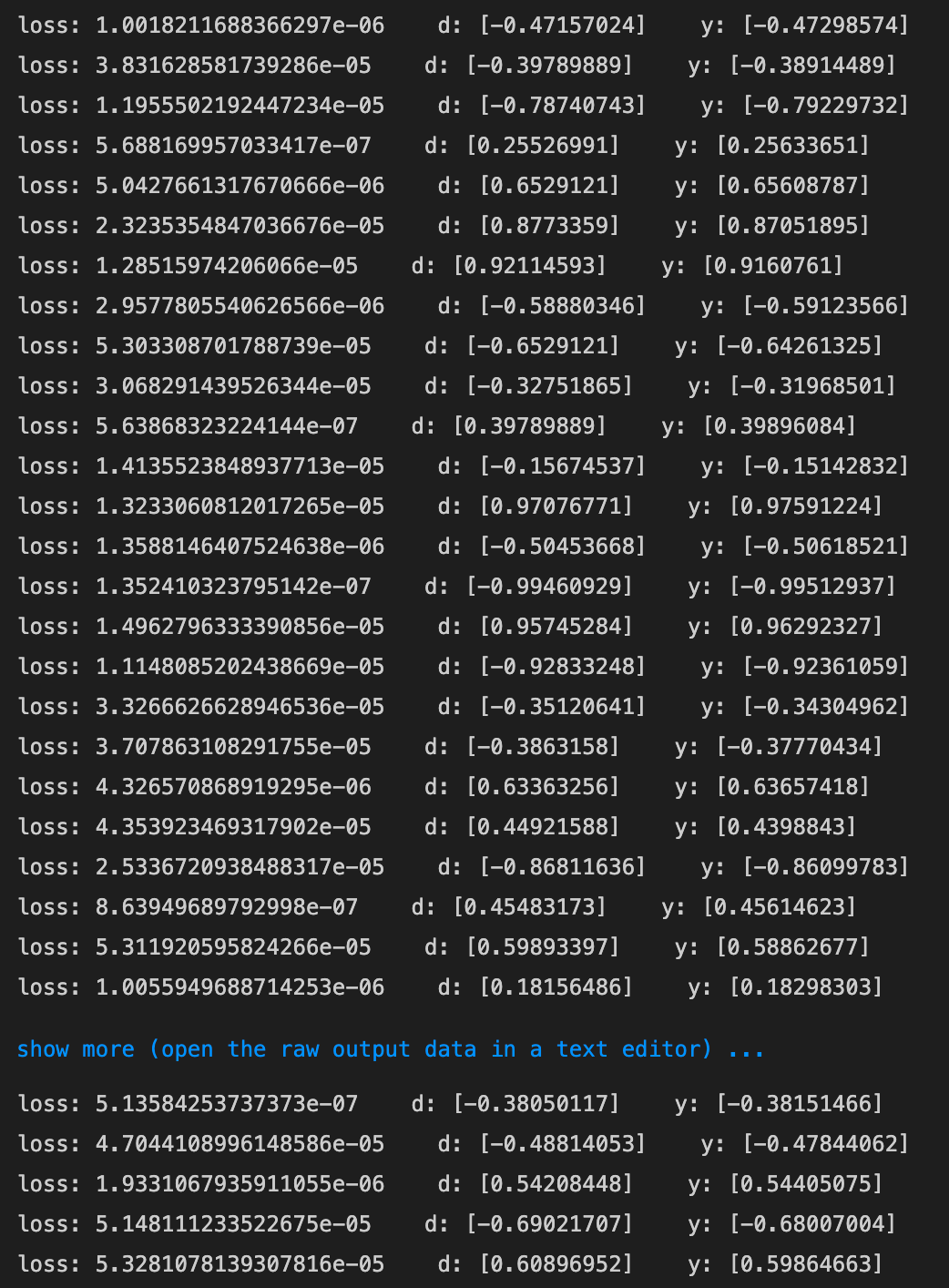
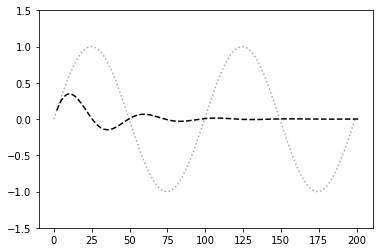
- 振幅が0に近づいてしまった
- [try] maxlenを5, iters_numを500, 3000(※時間がかかる)にしよう
- maxlenが5, iters_numが500のとき
- 周期が短くなった
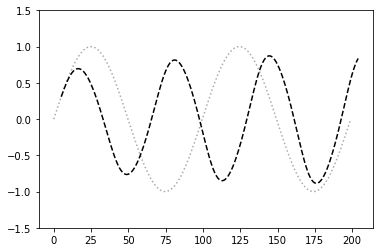
- 周期が短くなった
- maxlenが5, iters_numが3000のとき
- 元の波形とほぼ一致した
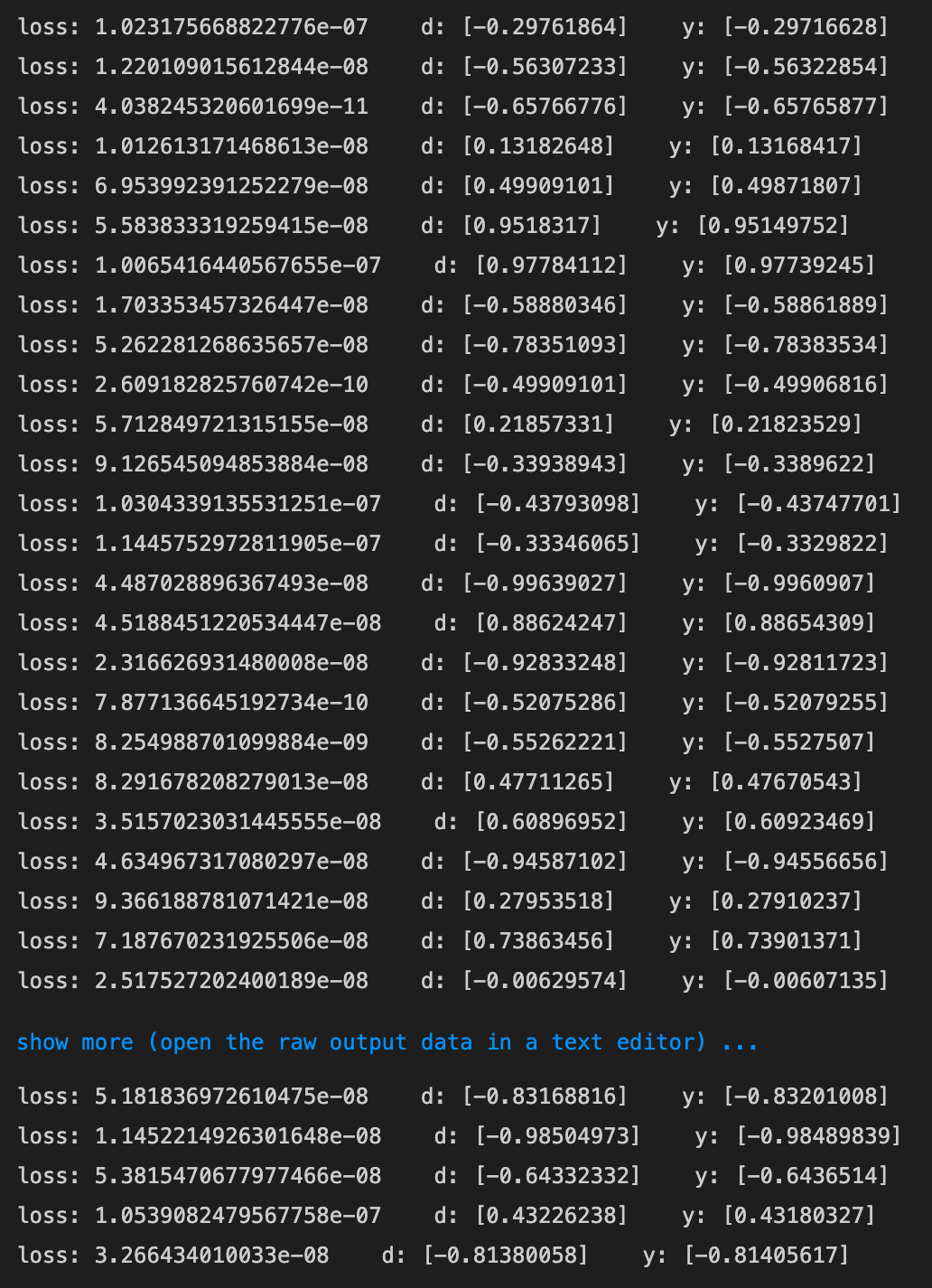
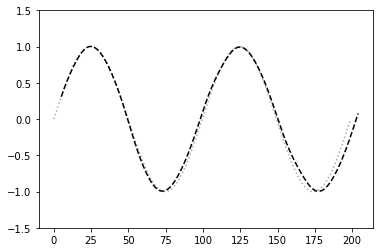
- 元の波形とほぼ一致した
- maxlenが5, iters_numが500のとき
